JPhysA编辑优选:精确求解一维玻色气体的动力学结构因子取得重要进展
文章介绍
Run-Tain Li (李润天), Song Cheng (程颂), Yang-Yang Chen (陈洋洋), Xi-Wen Guan (管习文)
通讯作者:
- 程颂,北京计算科学研究中心
- 陈洋洋,西北大学
- 管习文,中国科学院精密测量科学与技术创新研究院
研究背景:
由于维度和相互作用的共同影响,一维量子多体系统展现出诸多迥异于高维情形的有趣现象,比如Luttinger液体以及自旋-电荷分离等。关于动力学关联函数的研究一直是理解这些新奇量子多体现象的核心问题之一。然而,精确计算动力学关联函数一直是一个困难而复杂的问题。考虑到量子可积系统可以通过Bethe Ansatz方法严格求解,为理解量子多体系统的关联特性提供了精确计算方法。为此,借助形式因子方法,我们发展了一套简洁有效的算法可以用来精确计算动力学关联函数。精确地计算了在数千粒子尺度上的一维玻色气体(Lieb-Liniger模型)动力学结构因子。
研究内容:
Lieb-Liniger模型是最典型的一维量子可积系统,它描述了一维具有接触相互作用的无自旋玻色子气体。该模型可以利用Bethe Ansatz方法精确求解,体系的本征态可以利用一组类似无相互作用费米子的量子数标定。一般来说,利用谱表示计算动力学关联函数需要考虑所有的本征态对形式因子的贡献并求和。因此,计算大尺寸系统关联函数的核心困难是如何找出具有显著贡献的本征态并有效的截断求和。
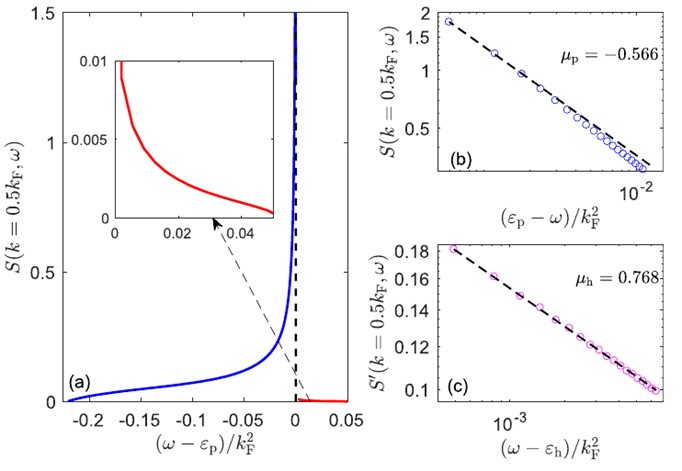
为此,我们提出用4个具有显著物理意义的量子数标注(非负整数)来划分本征态的集合,事实证明这种划分能非常高效的筛选出了对关联函数贡献较大的状态,从而精确计算了色散关系阈值附近的结构因子幂律关系和非线性Luttinger液体的行为,其结果也确认了非线性Luttinger液体理论预言的正确性。这表明在该尺寸下体系的关联性质已经接近热力学极限,展现了量子多体关联的本质。此外,我们还与其他理论方法进行了对比,结果显示我们的方法具有极高的精度,尤其是正确地反映了关联函数在谱边界上的幂律行为,参见图1。另外,我们的结果为其它方法提供了参考,参见图2 。

图1. 动力学结构因子的线形以及它在谱边界上的幂律行为,这里的系统粒子数N=2000,相互作用强度γ=1,激发动量k=0.5kF :(a) 动力学结构因子随激发能量的变化;(b) 单粒子谱的下边界上的幂律关系;(c) 单粒子谱的上边界上的幂律关系。注意,(b)和(c)均为对数坐标。
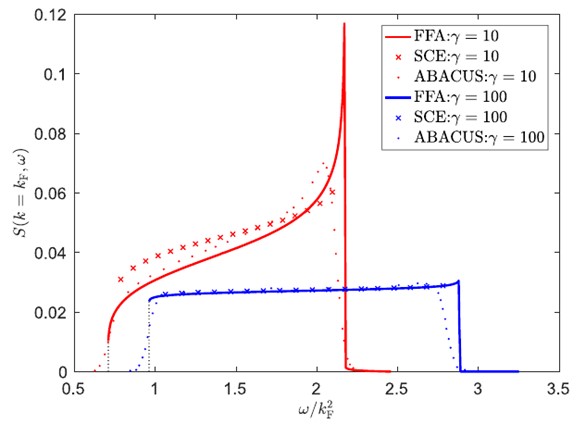
图2. 通过不同方法得到的动力学结构因子:FFA表示我们利用form factor approach得到的结果;SCE表示强相互作用展开(strong coupling expansion)的解析结果;ABACUS表示基于ABACUS库的数值方法。
期刊介绍

- 2022年影响因子:2.1 Citescore:4
- Journal of Physics A: Mathematical and Theoretical(JPhysA)每年出版50期,针对运用数学结构来描述物理世界的基本过程,并探索这些结构的分析、计算和数值方法。期刊内容涵盖:统计物理;非平衡系统、计算方法和现代平衡理论;混沌和复杂系统;数学物理;量子力学和量子信息理论;场论和弦理论;流体和等离子体理论;生物模型等方面。文章类型包括原创性论文和综述,以及关注于热点研究的专题综述和特刊,提供及时、全面的纵览。
