JPhysA编辑优选:朗道-齐纳跃迁概率的一种新的推导方法
文章介绍
Chen Sun(孙辰)
通讯作者:
- 孙辰,湖南大学物理与微电子科学学院
研究背景:
朗道-齐纳(LZ)模型是一个著名的严格可解的含时量子模型,它描述了二能级系统在线性驱动下的非绝热跃迁。自1932年被提出以来,LZ模型成为了许多更复杂的量子模型的基础,目前已在多类物理体系如量子点、超导量子比特等中获得了实现和应用。LZ的模型的跃迁概率有多种推导方法,这些方法大多依赖复杂的数学工具,如特殊函数、拉普拉斯变换等,而一些简单的推导方法,如准经典分析方法、马尔可夫近似等则用到了近似,因而并不是严格的。因此,寻求一种简单且严格的推导方法具有重要意义。本工作基于函数方程与可积性得出了LZ跃迁概率的一种新的推导方法,此方法无需用到复杂的数学,且推导过程完全严格。
研究内容:
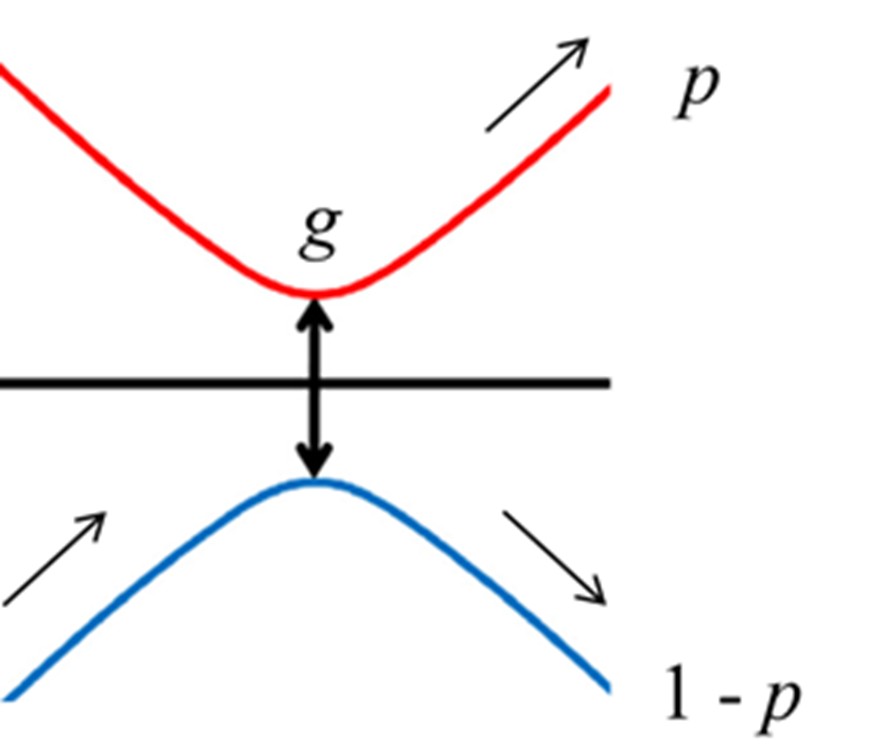
朗道-齐纳(LZ)模型是描述二能级系统在线性驱动下的非绝热跃迁的典型模型。其哈密顿量为 H = btσz+gσx(其中σz与σx为泡利矩阵),其能级随时间t的变化如下图所示。这一模型从t=-∞到+∞的演化的非绝热跃迁概率满足LZ公式:p = exp(–πg²/b)。LZ公式的严格推导方法大多依赖复杂的数学工具,如特殊函数、拉普拉斯变换等。

本工作为LZ公式的指数形式提供了新视角,即这一指数形式可以由柯西指数函数方程的解而得到。同时也揭示了LZ公式与含时量子模型的可积性的联系,即LZ公式可视为可积性的结果,尽管二能级LZ哈密顿量本身并不满足可积性条件。总之,本工作的重要性在于提供了一种LZ公式的新的严格推导方法,加深了对LZ公式数学结构的理解,并扩展了可积性概念的应用范围。
作者介绍

孙辰 教授
湖南大学
- 孙辰,湖南大学教授。从事凝聚态及量子物理理论研究。近期主要研究方向为寻找严格或近似可解的含时量子多体系统(特别是多能态朗道-齐纳模型),研究这样的系统中的物理现象,并探索其可能的应用。在Phy. Rev. Lett.、Phy. Rev. B、J. Phys. A: Math. Theor.等学术期刊发表论文三十余篇。
期刊介绍

- 2024年影响因子:2.1 Citescore:3.8
- Journal of Physics A: Mathematical and Theoretical(JPhysA)每年出版50期,针对运用数学结构来描述物理世界的基本过程,并探索这些结构的分析、计算和数值方法。期刊内容涵盖:统计物理;非平衡系统、计算方法和现代平衡理论;混沌和复杂系统;数学物理;量子力学和量子信息理论;场论和弦理论;流体和等离子体理论;生物模型等方面。文章类型包括原创性论文和综述,以及关注于热点研究的专题综述和特刊,提供及时、全面的纵览。
