JPCM编辑优选:华中科技大学发表半导体能带算法长篇综述

文章介绍
通讯作者:
- 薛堪豪,华中科技大学集成电路学院
近期,应IOP出版社旗下Journal of Physics: Condensed Matter期刊编辑的邀请,华中科技大学集成电路学院缪向水、薛堪豪团队撰写了关于DFT-1/2以及shell DFT-1/2新型能带计算方法的长篇综述论文。这篇38页的论文DFT-1/2 and shell DFT-1/2 methods: electronic structure calculation for semiconductors at LDA complexity回顾了固体能带计算的历史,分析了密度泛函理论带隙问题的根源,建立各种解释之间的联系。特别是,针对巴西圣保罗大学费雷拉教授等人于2008年提出的DFT-1/2能带计算方法,薛堪豪教授等人从固体的基本哈密顿量出发进行了详细的数学推导,特别是强调了其自能势形式的物理来源,推导过程的变量标记与Richard Martin的Electronic Structure经典论著严格保持一致。文章阐明了薛堪豪教授于2018年提出的shell DFT-1/2改进方法的基本思路与其应用效果,并介绍了DFT-1/2的其他重要发展。在带隙修正的层面上,我们还比较了DFT-1/2与杂化泛函、sX-LDA、GW、电子自相互作用修正(SIC)、Koopmans-compliant泛函、剪刀算符、DFT+U、Delta-sol等其他方法之间的联系与区别。论文展示了(shell) DFT-1/2是特别适合于微电子、光电子等领域的半导体能带计算方法,列举了诸多成功应用实例,并分析了方法可能的局限性。该论文将吸引更多学者关注DFT-1/2与shell DFT-1/2计算方法,拓展其具体应用,并为方法的进一步发展指明方向。
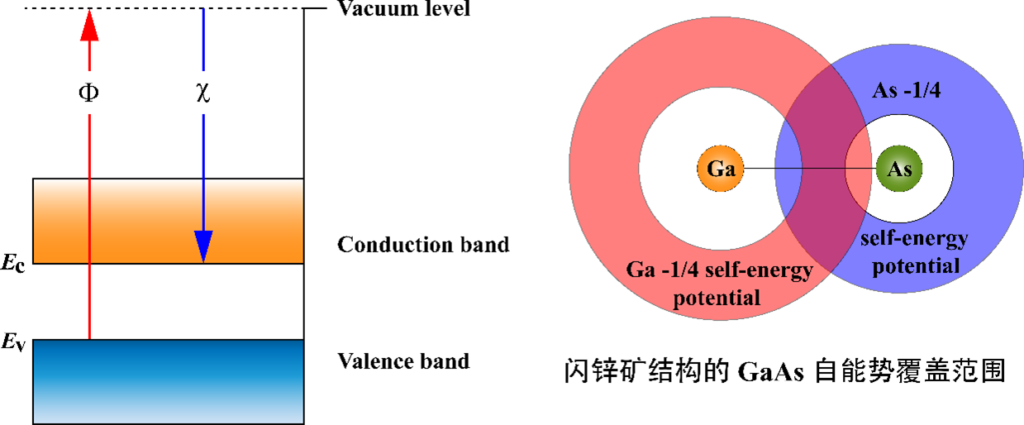
图1.半导体带隙的定义(φ-χ)以及shell DFT-1/2的实空间自能修正
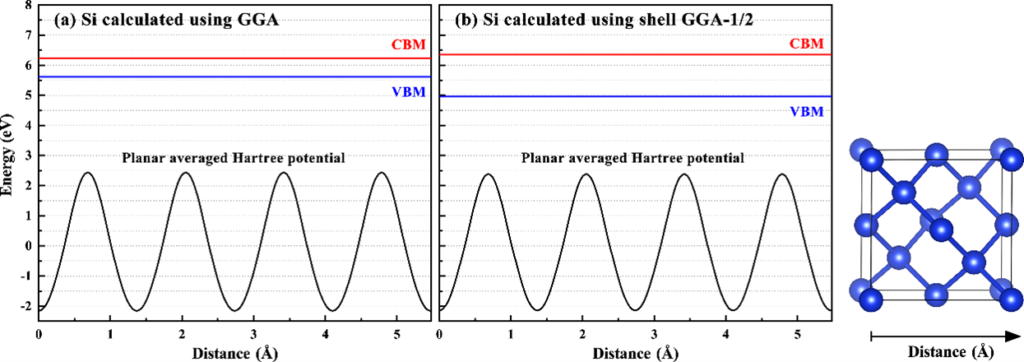
图2.普通GGA与shell GGA-1/2计算出的单晶硅电势与带边位置
研究背景:
带隙是半导体最重要的基本参数,其大小与类型(如直接带隙或间接带隙)在很大程度上决定了半导体的功用。然而,在半导体能带结构中,带隙的准确计算具有相当的难度。目前半导体物理教材广泛引用的硅、锗、砷化镓等能带结构主要源于1976年Chelikowski和Cohen基于经验赝势的计算。然而,精确的能带图仍然依赖于光学吸收以及低温回旋共振等实验结果的输入。完全从量子力学第一原理出发精确还原出半导体的能带结构仍然是一项艰巨的任务。密度泛函理论是当今最为流行的第一原理计算方法,其计算半导体的基态特性精度较高,但对于牵涉到激发态的带隙的计算,在其常用的局域密度近似(LDA)以及广义梯度近似(GGA)下,存在带隙被系统性低估的问题,其偏差平均可达到 40%。
对于分子的计算,量子化学领域采用计算量较高的杂化泛函,双杂化泛函以及多体微扰等方法,取得了良好的精度。然而,在微电子、光电子领域中,对半导体进行能带计算主要目的并非得到其带隙值等基本参数(这些参数实验上容易获得),而是探索半导体中的杂质、缺陷、各种应变状态、表面、界面等对其电子结构的影响。因此,势必需要建立包含几百个原子的超原胞进行计算,这将同时要求计算方法具有较高的效率,并能准确还原带隙等参数,对方法提出了苛刻的限制条件。
事实上,密度泛函理论本身的不断改进,主要是针对体系基态特性的改进,而在Kohn-Sham框架下获得的能量本征值,即使泛函较为精确,亦只能解释为基态特性。半导体的带隙则牵涉到激发态的性质,例如本征激发涉及到一整个电子的激发(而不是无穷小的电荷的激发),并在价带留下一个空穴,过程中体系的电子数可变。准粒子语言才是描述这种过程的恰当的物理工具。然而,在计算材料学和工程研究中,经常希望能将Kohn-Sham的能量本征值解释为电子能带结构。这种期望虽然严格来说并不妥当,却有深厚的应用需求以及相当的合理性。例如杂化泛函也只是对基态进行计算,其预测的半导体带隙值却有很大的改进,虽然其对于带隙较大的绝缘体仍然存在带隙低估的问题。另外,Perdew小组于2015年提出的SCAN泛函(Phys. Rev. Lett. 115, 036402),是一类满足多达17种约束条件的meta-GGA泛函,其计算精度亦得到广泛认可。然而,meta-GGA由于计算出的仍然是普通电子结构而非准粒子结构,在某些体系下的带隙值仍然可能被低估。近期关于InAs/GaSb超晶格的计算显示,SCAN泛函仍可能将窄带隙的超晶格半导体错判为金属(Phys. Rev. Applied 18, 024058),而shell DFT-1/2则可以较好地还原出该系列超晶格半导体的能带结构与带隙。shell DFT-1/2源自DFT-1/2,这类计算方法采取了完全不同的策略,乃是对激发过程中的过渡态进行计算,因此本质上可以与准粒子结构建立联系,但名义上又与基态计算有相同的复杂度,因此具有较好的速度以及较高的带隙精度。遗憾的是,DFT-1/2自从2008年被提出之后(Phys. Rev. B 78, 125116),其初期的应用并不很广泛,只是在近年来才开始获得重视以及得到广泛的应用。其原因之一是方法的推导过程较为简略,特别是自能势方案的严格推导和论证有缺失之处。在该方法的应用方兴未艾,但理论基础仍存在某些质疑的情况下,非常有必要重新对该方法进行数学推导、详细归纳出其牵涉的诸物理假定,对其适用性进行综合评估,并对方法的未来发展趋势进行展望。
作者介绍

薛堪豪 教授
华中科技大学
- 薛堪豪,华中科技大学集成电路学院教授,博士生导师,入选湖北省教育厅“楚天学者”人才计划。本科与硕士分别毕业于清华大学电子工程系与清华大学微电子学研究所,荣获2007年清华大学优秀硕士毕业生。2007年8月至2010年5月于美国科罗拉多大学珂泉分校攻读博士学位,获科罗拉多大学2010年优秀毕业生。在Science, Nature Communications, Physical Review Letters等国际期刊上发表论文115篇,其中一作、通讯(含共同通讯)发表60篇。研究领域主要包括半导体能带计算方法、基于二氧化铪的微纳电子器件、光电探测器等。
期刊介绍

- 2021年影响因子:2.745 Citescore: 4.3
- Journal of Physics: Condensed Matter (JPCM)为读者提供凝聚态物理、软物质、纳米科学和生物物理各领域的最新研究成果。JPCM发表实验/理论分析和模拟研究,读者可以获取涉及下列领域的专题综述、快报和特刊:表面、界面和原子尺度的科学,液体、软物质和生物物理,纳米材料和纳米电子,固体结构的晶格动力,电子结构,超导体和金属、半导体,电介质和铁电,以及磁学与磁性材料。
