JPhysA编辑优选:自旋-轨道耦合自旋-1 BEC中的孤子碰撞
文章介绍
Juan-juan Qi(祁娟娟), Dun Zhao(赵敦) and Wu-Ming Liu(刘伍明)
通讯作者:
- 赵敦,兰州大学数学与统计学院
研究背景:
孤子态是玻色-爱因斯坦凝聚体中宏观量子效应的典型表现形式,自旋-轨道耦合为玻色-爱因斯坦凝聚体中孤子态的产生和调控提供了重要的新途径,因此对自旋-轨道耦合玻色-爱因斯坦凝聚体中孤子动力学的研究成为近年来超冷原子领域研究的重要课题之一。本文的目的是利用解析解,在理论上研究自旋-轨道耦合效应对系统孤子碰撞动力学的影响,为相关实验提供参考。
研究内容:
本文应用非标准的Hirota双线性方法,得到了一维的自旋-轨道耦合自旋-1 玻色-爱因斯坦凝聚体系统的一系列精确的单孤子和双孤子解,研究了自旋-轨道耦合效应对系统的孤子动力学,特别是孤子碰撞动力学的影响,详细讨论了极化-铁磁型、铁磁-铁磁型和极化-极化型的孤子碰撞的动力学性质,比较了自旋-轨道耦合效应存在和不存在时系统的孤子态的差异。一个有趣的结果是:自旋轨-道耦合效应可以导致孤子的分裂。由于孤子态及孤子碰撞可以在实验中观测,本文的结果为可能的实验提供了理论依据。
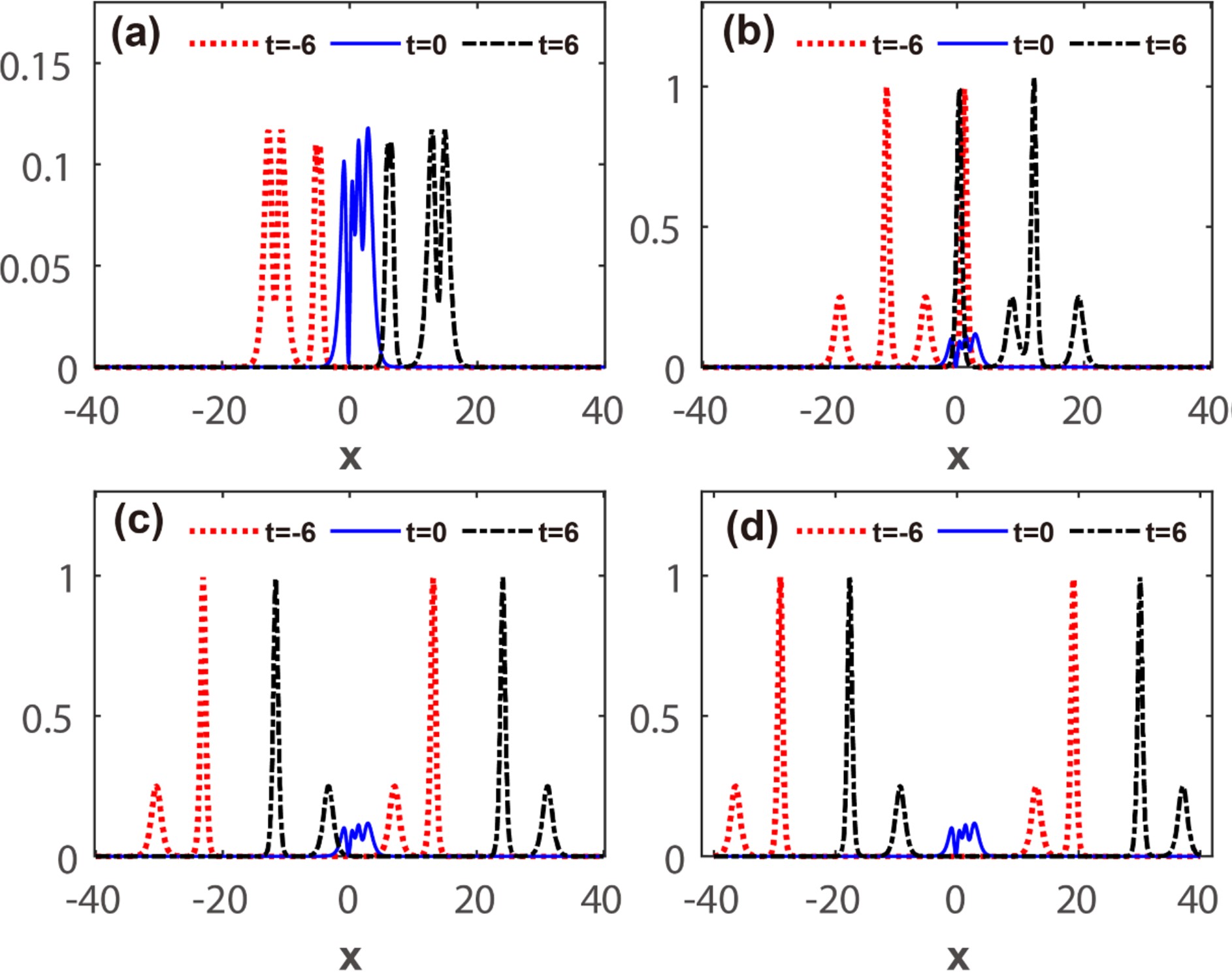
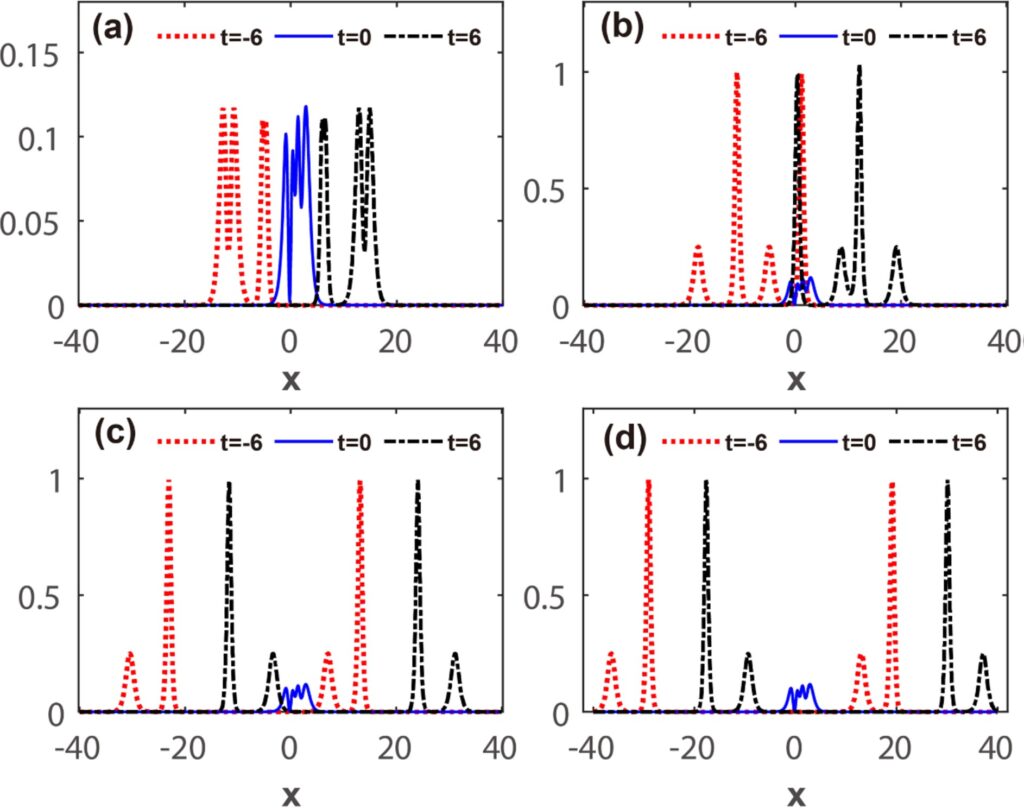
文中图2清楚显示了自旋-轨道耦合效应对系统的孤子碰撞动力学的影响。
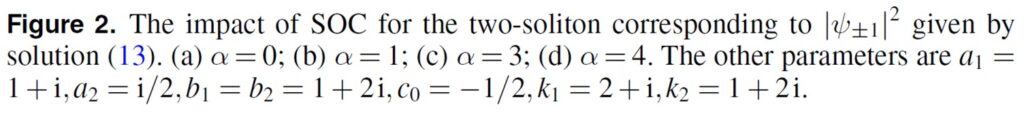
期刊介绍

- 2022年影响因子:2.1 Citescore:4
- Journal of Physics A: Mathematical and Theoretical(JPhysA)每年出版50期,针对运用数学结构来描述物理世界的基本过程,并探索这些结构的分析、计算和数值方法。期刊内容涵盖:统计物理;非平衡系统、计算方法和现代平衡理论;混沌和复杂系统;数学物理;量子力学和量子信息理论;场论和弦理论;流体和等离子体理论;生物模型等方面。文章类型包括原创性论文和综述,以及关注于热点研究的专题综述和特刊,提供及时、全面的纵览。
