JPCM编辑优选:三维声子晶体中的类平方根高阶拓扑态

本篇研究来自华中科技大学祝雪丰课题组。本文介绍了在平方根晶体中引入不同类型层间耦合,将平方根拓扑态推广到三维声拓扑,在更高维度上展现和操控平方根拓扑态,实现三维声子晶体中不同频段高阶拓扑边界态,启发新型声学拓扑功能器件的设计。
文章介绍
Zhi-Guo Geng(耿治国), Yu-Gui Peng(彭玉桂), Huanzhao Lv(吕欢兆), Zhan Xiong(熊展), Zhaojiang Chen(陈赵江), Xue-Feng Zhu(祝雪丰)
通讯作者:
- 祝雪丰,华中科技大学
该工作从二维平方根拓扑声子晶体出发,通过垂直堆垛单层二维晶体引入层间耦合,在三维结构中构建出类平方根拓扑声子晶体,进而实现不同维度高阶拓扑态。
周期堆垛的类平方根拓扑晶体保留了二维平方根拓扑晶体的手征对称性特征,具有不同的体带隙,在不同体带隙中出现了拉长的表面态和棱态。
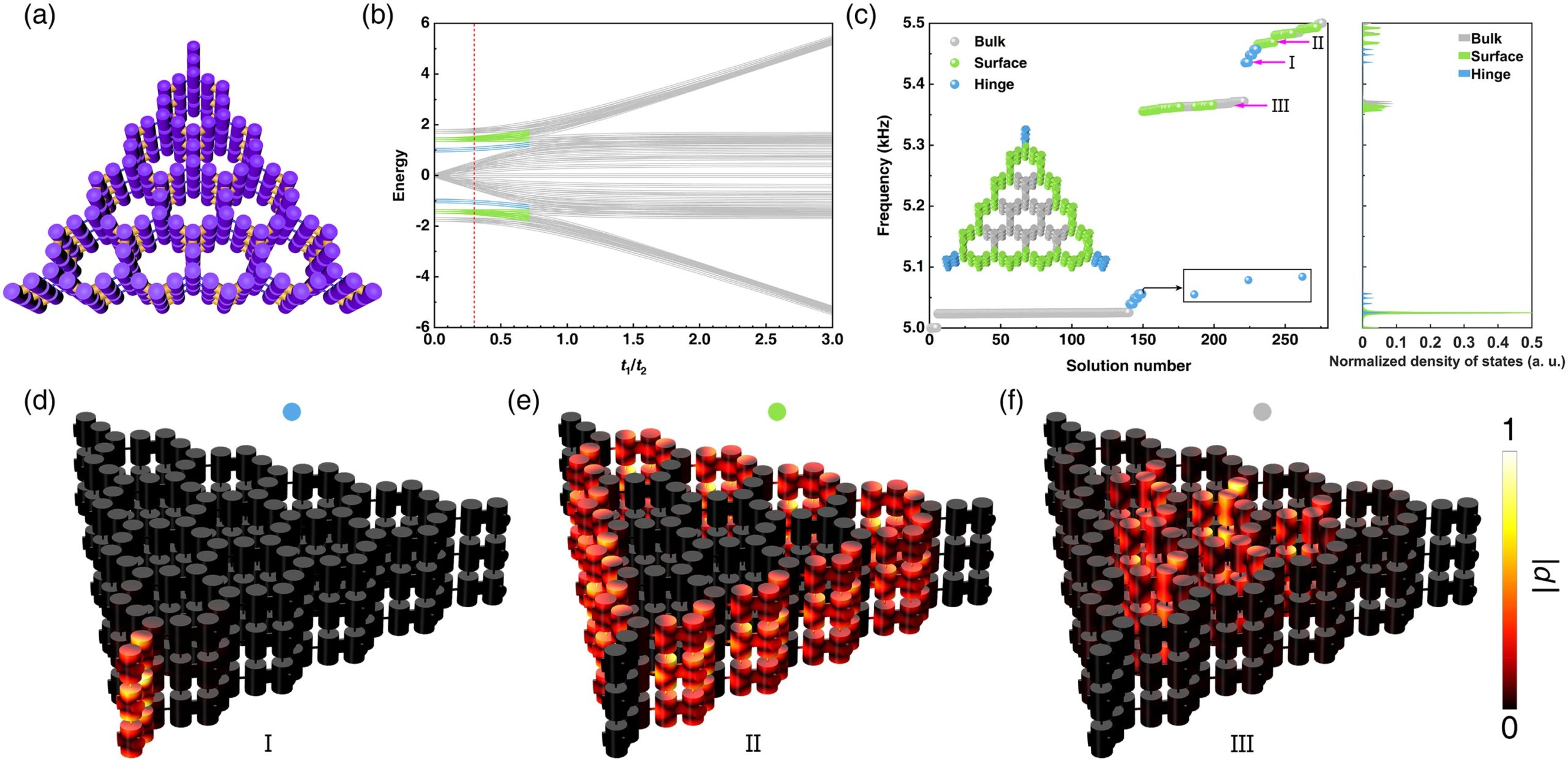
图1. 声学类平方根拓扑态。
这类拓扑态本质上是面内拓扑效应在z方向的延伸,因而拓扑态在晶体边界是可调的,允许被裁剪和设计。
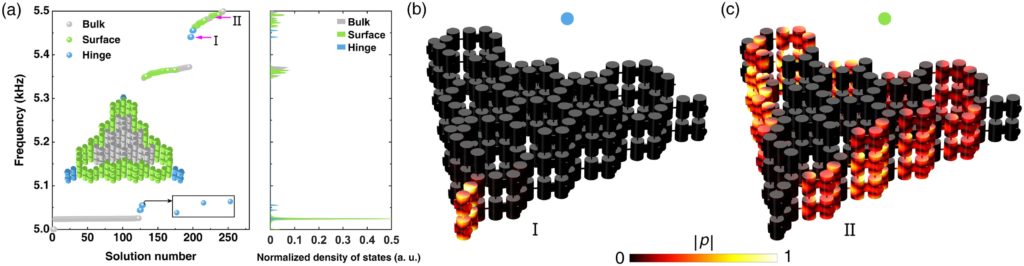
图2. 可调的声学类平方根拓扑态。
我们进一步在二维晶格间引入交错的层间耦合,晶格沿z方向产生非平庸的体极化,实现了声学三阶拓扑角态。
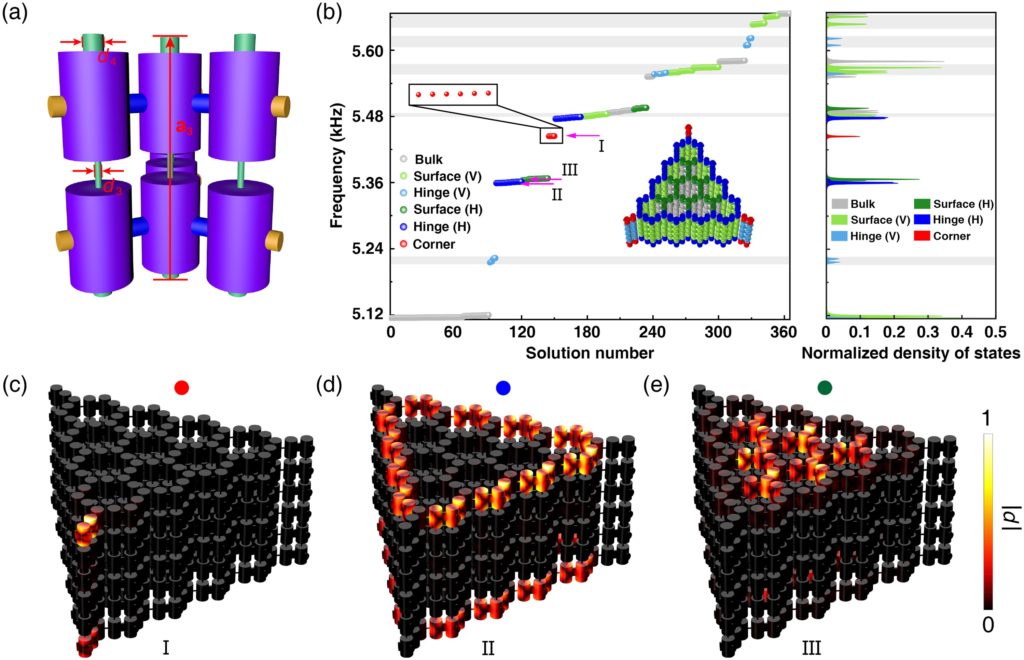
图3. 层间交错耦合诱导的声学三阶拓扑态。
值得一提的是,该工作利用紧束缚计算和数值模拟对高阶拓扑态的鲁棒性进行了系统论证,对比边界态微扰和体微扰证实了高阶拓扑态对体微扰的强鲁棒性。
该工作将平方根拓扑态拓展到三维声子晶体中,丰富了声学拓扑态的构建方案,并有利于实现不同频段的新原理声学器件。
研究背景:
平方根拓扑态的非平庸拓扑性质继承自哈密顿量的平方,即父代晶格哈密顿量。在拓扑晶格格点间嵌入新的格点(开平方操作)即可获得平方根拓扑晶体,其晶格对称性特征允许出现成对的拓扑态。目前,二维平方根拓扑态已在电路、声学和光学等人工周期系统中实现。本工作通过在平方根晶体中引入不同类型的层间耦合,将平方根拓扑态推广到三维声拓扑领域,在更多维度上展现和操纵平方根拓扑态,实现三维声子晶体中不同频段的高阶拓扑边界态,启发新原理声学功能器件的设计。
作者介绍

祝雪丰 教授
华中科技大学
- 祝雪丰,华中科技大学物理学院/创新研究院教授,国家重点研发计划项目负责人。主要从事微纳超声人工结构器件、拓扑声和热调控等相关研究工作。2011年博士毕业于南京大学物理学院声学所,师从程建春教授。2012至2014年在加州大学伯克利分校张翔院士课题组从事研究工作。担任Chin. Phys. Lett.、Chin. Phys. B、《物理学报》和《物理》四刊青年编委。
期刊介绍

- 2021年影响因子:2.745 Citescore: 4.3
- Journal of Physics: Condensed Matter (JPCM)为读者提供凝聚态物理、软物质、纳米科学和生物物理各领域的最新研究成果。JPCM发表实验/理论分析和模拟研究,读者可以获取涉及下列领域的专题综述、快报和特刊:表面、界面和原子尺度的科学,液体、软物质和生物物理,纳米材料和纳米电子,固体结构的晶格动力,电子结构,超导体和金属、半导体,电介质和铁电,以及磁学与磁性材料。
