MLST编辑优选:动力系统深度学习方法预测无穷维非线性系统
文章介绍
通讯作者:
- 李建平,中国海洋大学深海圈层与地球系统前沿科学中心/物理海洋教育部重点实验室/未来海洋学院/海洋与大气学院/海洋碳中和中心、青岛海洋科技中心海洋动力过程与气候功能实验室
研究背景:
非线性混沌动力系统的预测是世界性的科学难题。1980年代,Takens等提出延迟嵌入定理,推动了预测有限维混沌系统的相空间重构技术发展。2024年,李建平团队基于该定理,提出了DSDL理论与方法,在对Lorenz’ 63系统等有限维非线性混沌系统的预测中取得突破,预测性能超越现有机器学习方法,并通过提取关键变量,为解决“黑匣子”问题提供了一种新的方案。
然而,大气、海洋等实际系统多受偏微分方程(PDEs)控制的无穷维动力系统(IDDS)支配。2005年,Robinson发展了适用于PDEs的嵌入理论,在理论上解决了延迟嵌入定理对PDEs的适用性,不过,其逆向映射能否通过DSDL建模实现PDEs的有效预测尚不得而知。因此,DSDL理论与方法对非线性混沌系统的预测研究不应仅局限于有限维系统,而应拓展到IDDS领域。
研究内容:
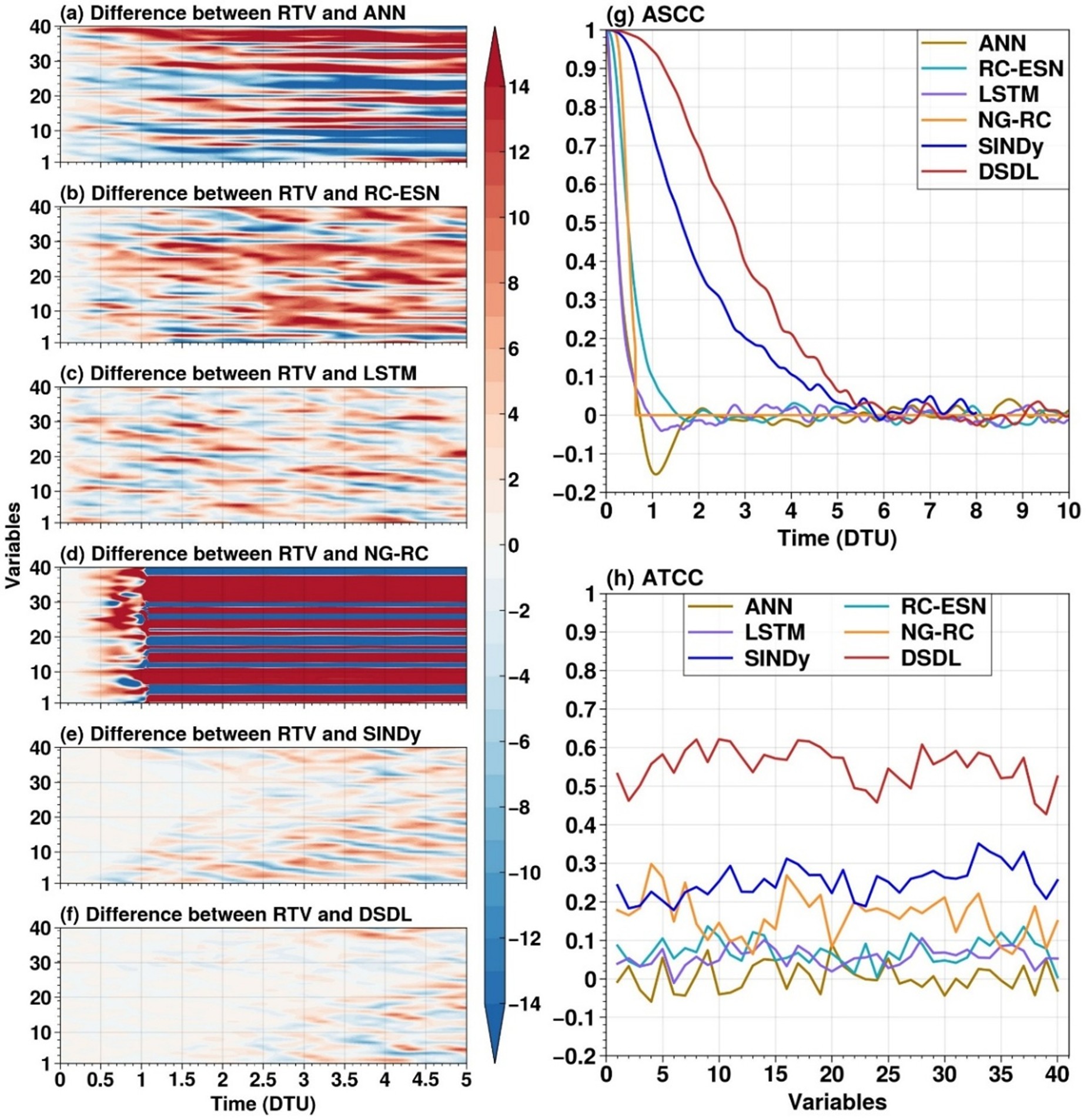
为探究DSDL理论和方法预测PDEs方程的可行性和能力,本研究选取了具有时空分布特征的Lorenz’ 96系统和Kuramoto-Sivashinsky (K-S)偏微分方程系统作为预测对象,将DSDL方法与目前认可度较高的机器学习方法(如:ANN、RC-ESN、LSTM、NG-RC、SINDy等)进行了对比,结果发现,在对两种系统进行预测时,DSDL方法预测性能表现优越,预测结果与系统的参考真值(RTV)吻合较好,其中,DSDL方法对K-S方程的有效预测时长可达225个无量纲时间,预测性能远超其他方法(图1和图2),这说明DSDL理论与方法适用于PDEs控制的IDDS,同时能够提取关键变量,并做出有效预测。
此外,对各类混沌系统进行长期预测的统计结果表明,DSDL方法仍具有显著优势,尤其在概率密度分布的尾部,DSDL方法的预测结果与RTV吻合较好,表明其具有一定的预测极端事件的能力(图3)。同时,DSDL方法在预测随外部强迫和变量数目更改(即混沌属性变化)的Lorenz’ 96系统时,表现出随系统混沌属性降低,预测效果增强的情况(图4),这表明DSDL方法的预测符合混沌动力学理论,具有数理理论的支撑。
上述研究凸显了DSDL方法在无穷维非线性混沌动力系统预测方面的适用性和显著优势,为未来实现在大气、海洋等现实世界PDEs系统的DSDL建模预测提供了坚实的理论基础和技术支撑,也为解决这类复杂系统的预测难题开辟了新的路径。
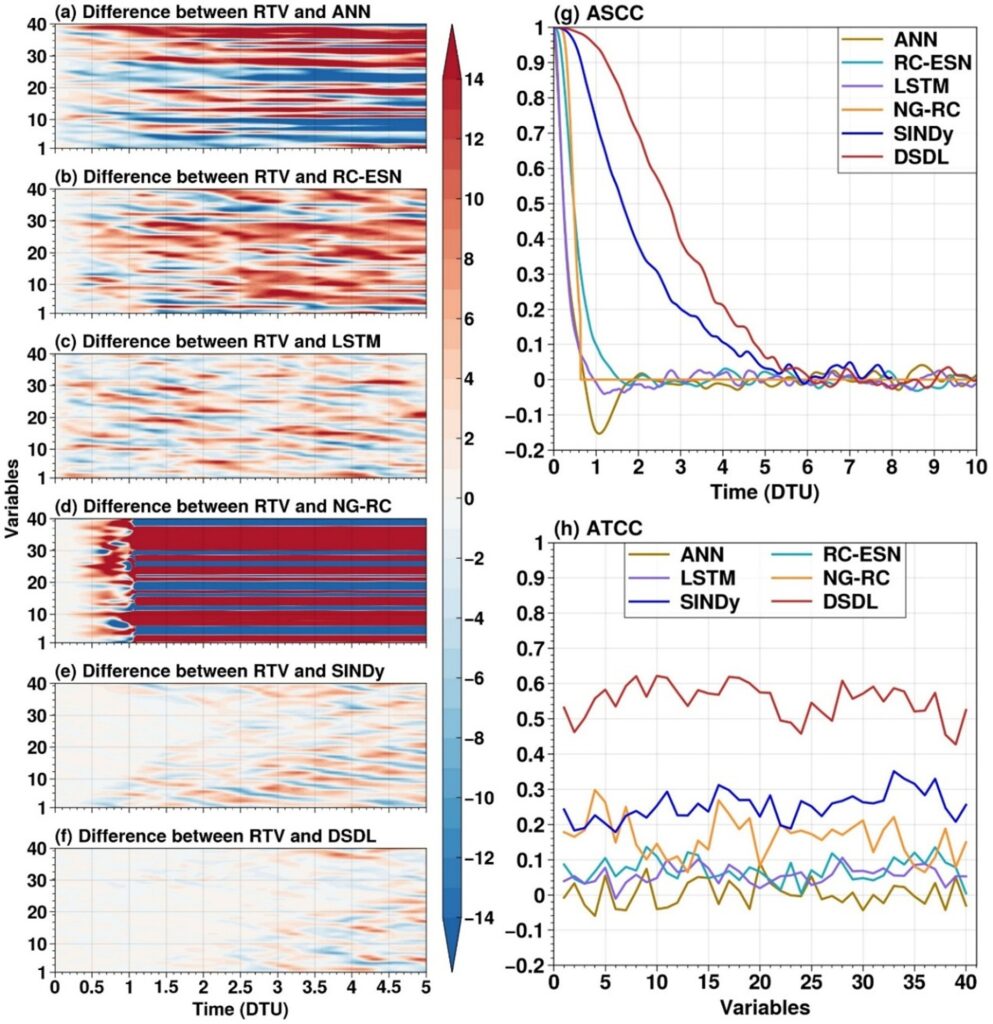
图1 DSDL方法与其他深度学习方法对Lorenz’ 96系统预测效果的比较
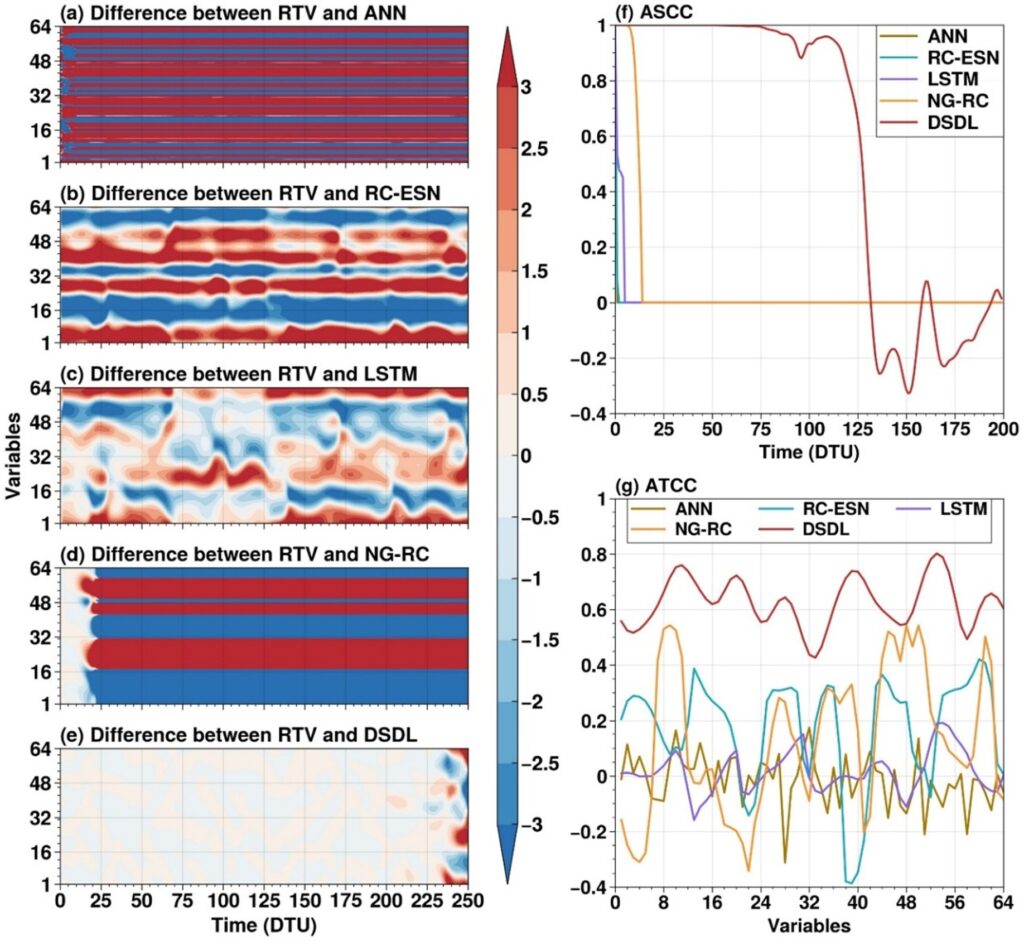
图2 DSDL方法与其他深度学习方法对K-S方程预测效果的比较
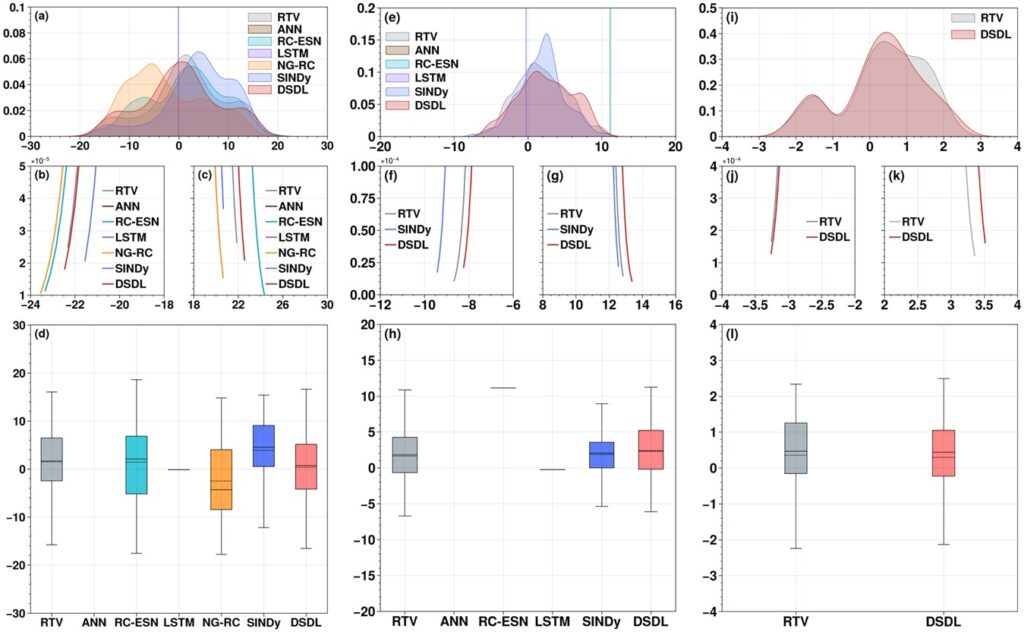
图3 DSDL方法与其他深度学习方法对Lorenz’ 63系统、Lorenz’ 96系统和K-S方程长期预测统计特征的比较
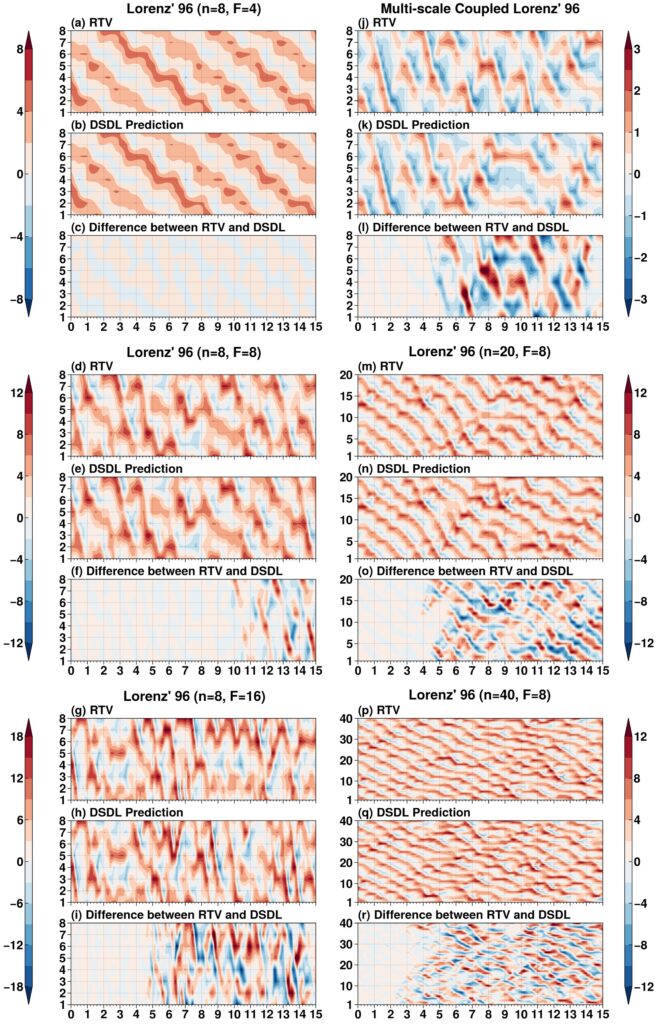
图4 DSDL方法对不同混沌属性的Lorenz’ 96系统预测效果的比较
作者介绍

李建平 教授
中国海洋大学
- 李建平,中国海洋大学特聘教授、未来海洋学院院长、国家杰青、国家973和重大研究计划项目首席、国际气候与环境变化委员会(CCEC)主席、国际气候学委员会(ICCL)主席、国际IUGG会士、Climate Dynamics执行主编、获国家自然科学二等奖(排名第3)、政府特殊津贴、爱思唯尔中国高被引作者、斯坦福大学全球前2%顶尖科学家榜单等。从事气候学研究,发表论文500余篇。
期刊介绍

- 2024年影响因子:4.6 Citescore:7.7
- Machine Learning: Science and Technology (MLST)是一本跨学科期刊,致力于发表智能机器在物理、材料科学、化学、生物学、医学、地球科学、天文学和工程学等多学科领域的应用和发展。涉及领域包括:物理学和空间科学;设计和发现新材料和分子;材料表征技术;模拟材料、化学过程和生物系统;原子和粗粒度模拟;量子计算;生物学、医学和生物医学成像;地球科学(包括自然灾害预测)和气候学;模拟方法和高性能计算。同时,也包括机器学习方法在概念上的新进展:新的学习算法;深度学习架构;核心方法;概率和贝叶斯方法;生成方法;强化和主动学习;经常性和基于时间结构的方法;神经启发方法(包括神经形态计算)。
