Journal of Optics编辑优选：Zernike多项式及其应用

图1 Frits Zernike（1888-1966），物理学家和数学家，因发明相衬显微镜获得1953年诺贝尔物理学奖

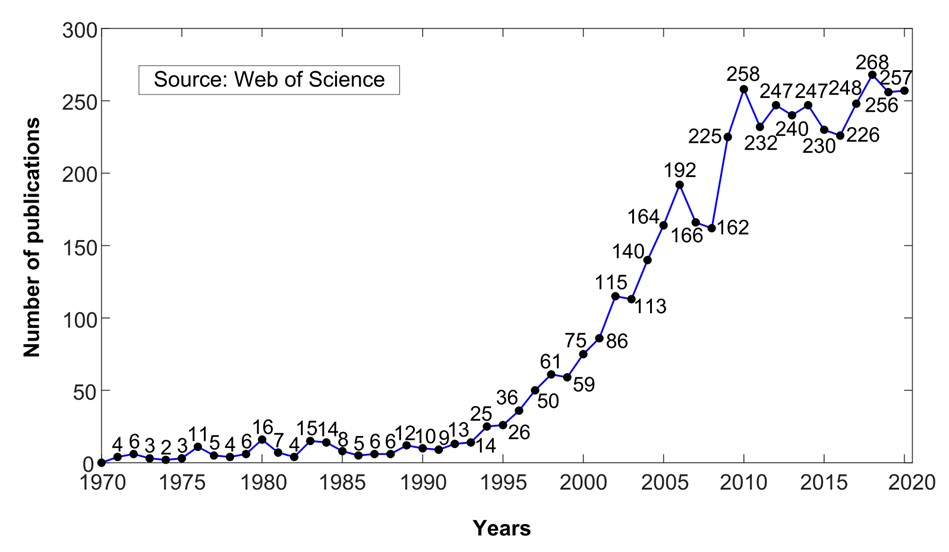
图2 1970至2020年间与Zernike多项式相关的论文出版数量

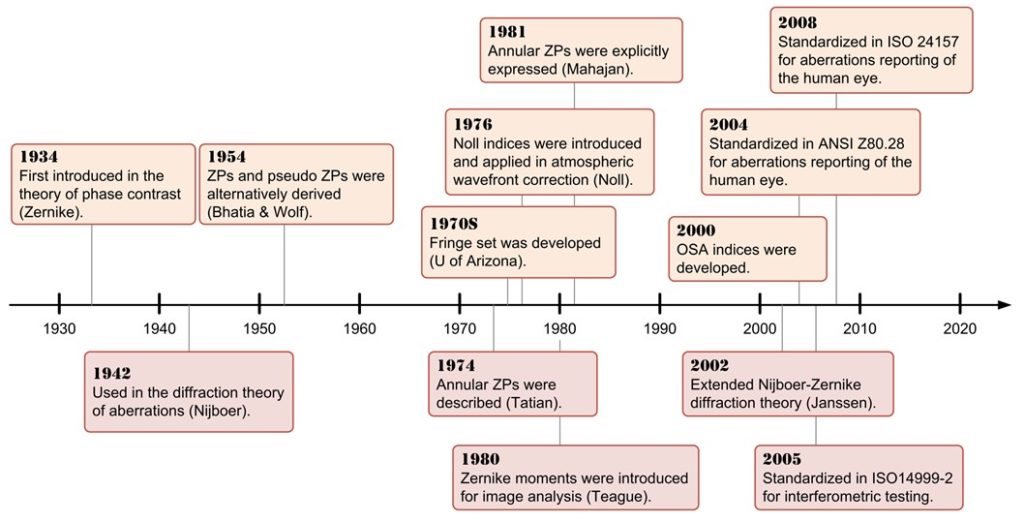
图3 Zernike多项式发展历程中的里程碑事件

论文主要包括三个部分（见图4）。第一部分回顾了Zernike圆形多项式的六种不同索引方式，包括Noll索引（见图5）、OSA/ANSI索引、Fringe索引、ISO-14999索引、Born&Wolf索引以及Malacara索引，并对其进行了系统对比和分析；同时归纳了Zernike圆形多项式的数学性质，包括正交性、对称性、Fourier变换、积分变换、导数、递归关系等；讨论了Zernike多项式在波前拟合中的作用、不同孔径形状下Zernike多项式展开系数的变换与Seidel像差和Strehl比之间的关系；整理了Zernike多项式与XY单项式、Jacobi多项式、Legendre多项式、Bessel多项式、Chebyshev多项式、伪Zernike多项式等之间的关系。第二部分介绍了基于Gram-Schmidt正交化方法的非圆孔径Zernike衍生多项式的构造方法，包括环形、矩形、正方形、六边形、椭圆形等；重点讨论了Zernike环形多项式的定义、数学性质和在环形波前拟合中的作用。第三部分阐述了Zernike多项式在不同领域中的实际应用，包括衍射理论、光学设计、光学检测、眼视光学、自适应光学及数字图像分析等（见图6）。

论文旨在为初学者及领域研究人员提供一份关于Zernike多项式的完备参考指南，并促进Zernike多项式的进一步发展与应用。

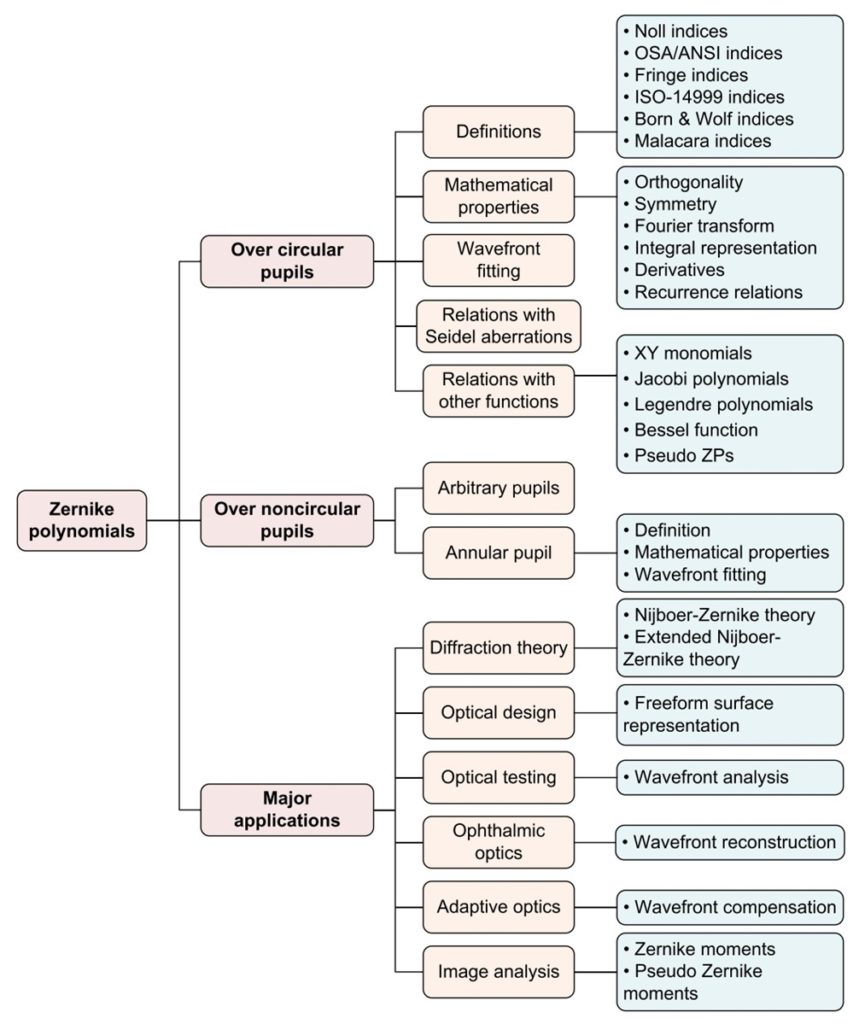
图4 论文主要讨论的内容

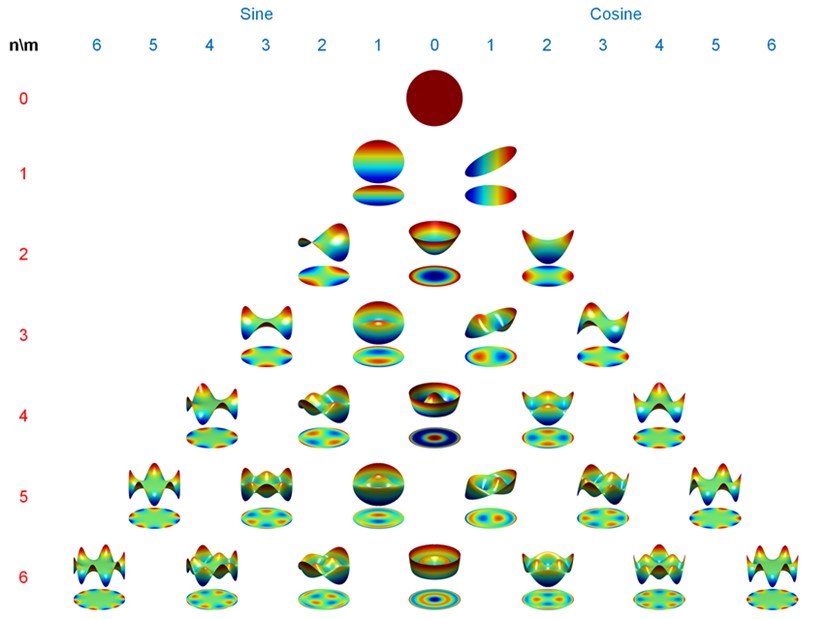
图5 Noll索引下的非归一化Zernike圆多项式（前6阶）

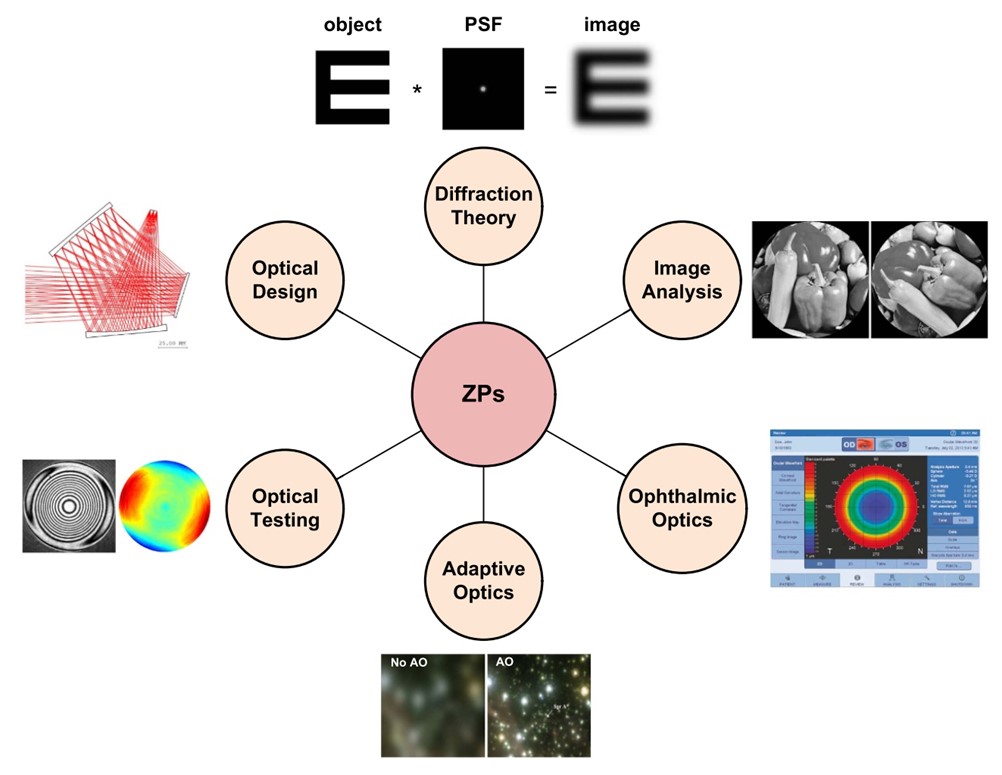
图6 Zernike多项式的主要应用

研究背景：

Zernike多项式是定义在单位圆域上的一组完备的连续正交函数。自1934年由Zernike提出以来，Zernike多项式在光学、眼视科学、图像处理等领域得到了广泛应用。但由于没有统一的定义，Zernike多项式有多种不同的索引方式并存，且数学性质缺乏系统的阐述。为了解决这一问题，本文系统性地回顾了圆形Zernike多项式及其非圆衍生多项式的发展历史、数学定义、基本性质、在波前拟合中的作用、与光学像差及其它相近多项式之间的关系。同时综述了Zernike多项式在衍射理论、光学设计、光学检测、眼视光学、自适应光学及图像分析等不同领域中的应用。由于数学性质简洁优美，Zernike多项式在科学研究及工业领域的应用预计会进一步扩大。该综述旨在为初学者及领域研究人员提供一份关于Zernike多项式的完备参考指南。