MLST编辑优选:(1+1)维偶子代分支湮灭随机游走的监督和无监督学习
文章介绍
Yanyang Wang(王艳阳), Wei Li(李炜), Feiyi Liu(刘非易) and Jianmin Shen(申建民)
通讯作者:
- 李炜,华中师范大学
研究背景:
机器学习(ML)已经被广泛应用于处理统计物理、高能物理、天文学等领域中的热点问题,特别是在处理相变上展现出强大的功能。不同于平衡相变,由于存在额外的时间维度,非平衡相变表现出更复杂和多样化的特征。在非平衡相变领域,一类反应扩散过程相变的普适类是令人关注的一大难题。相比于传统场论分析和蒙特卡洛模拟方法,ML具有成本低和精度高的优势。本工作尝试将一类监督学习与无监督学习模型应用到多种反应扩散过程中,从而探究系统的相变特征,为寻找新的普适类提供依据。通过分析无监督学习输出的物理意义,希望建立神经网络与物理系统的内在联系,以寻求ML在此类反应扩散系统中的广泛应用。
研究内容:
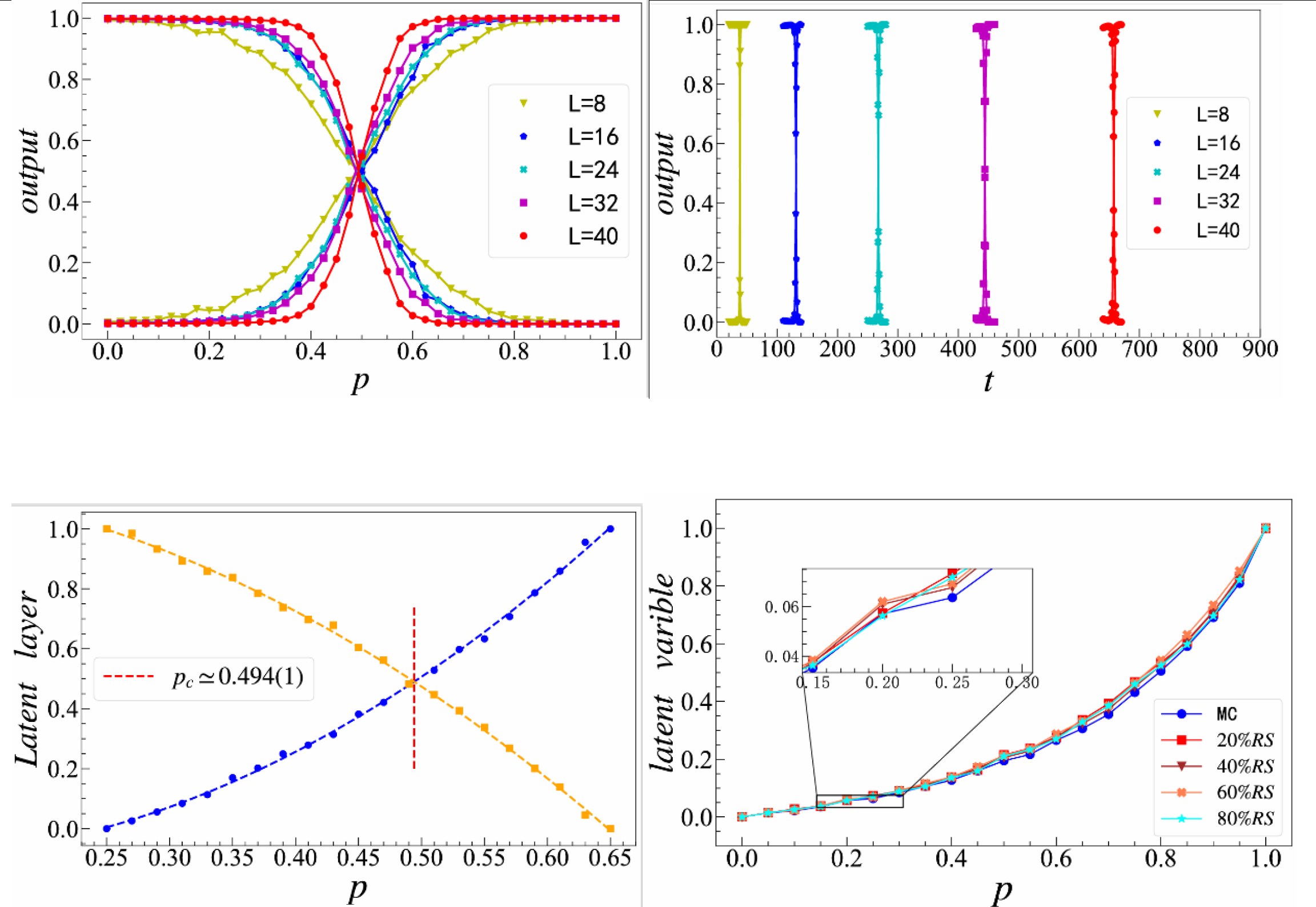
本文利用一般结构下的卷积神经网络预测了BAW模型不同系统尺寸下临界点的位置,得到了以分支概率表示的结果Pc=0.494(9),这与大尺寸的MC模拟结果非常接近。然后,本文利用不同演化时间步下的簇图来确定特征时间,得出动态指数为z=1.759(8)。此外,本文还测量了空间相关长度临界指数,根据有限尺寸标度律,结果为v⊥=1.83。这为偶数子代下的BAW过程普适类的分析提供了佐证。分析自编码的一维编码输出数据可以识别临界点为Pc=0.494(1)。本文还试图理解自编码的一维编码输出的物理意义。在系统噪声逐渐增加的情况下,发现自编码的一维编码输出仍然能够很好的反映系统的粒子密度。对于这类反应扩散系统,由于训练数据的充分性,ML可以使用簇图捕获更多关于系统的微观信息,这可以解释ML在准确识别此类系统的临界点和测量临界指数方面的有效性。鉴于实际计算能力的局限性,ML为研究非平衡相变的临界行为提供了一种新的方法。探索深度神经网络的输出与系统的序参量之间的关系,有助于开拓该方法在相变领域中的应用。
作者介绍

李炜 教授
华中师范大学
- 李炜,1974年出生于湖北荆州,2001年毕业于华中师范大学粒子物理研究所。主要研究方向:非平衡相变、演化博弈、复杂网络动力学。其中关于航空网的论文目前单篇他引已经超过600次;关于体育排名的研究被Nature和Science等国际重要科学杂志报道。国际合作单位包括美国Santa Fe研究所、德国马克斯-普朗克科学研究所。曾获得洪堡学者奖学金、全国百篇优秀博士论文提名奖、湖北省自然科学二等奖、湖北省青年科技奖等。
期刊介绍

- 2023年影响因子:6.3 Citescore:9.1
- Machine Learning: Science and Technology (MLST)是一本跨学科期刊,致力于发表智能机器在物理、材料科学、化学、生物学、医学、地球科学、天文学和工程学等多学科领域的应用和发展。涉及领域包括:物理学和空间科学;设计和发现新材料和分子;材料表征技术;模拟材料、化学过程和生物系统;原子和粗粒度模拟;量子计算;生物学、医学和生物医学成像;地球科学(包括自然灾害预测)和气候学;模拟方法和高性能计算。同时,也包括机器学习方法在概念上的新进展:新的学习算法;深度学习架构;核心方法;概率和贝叶斯方法;生成方法;强化和主动学习;经常性和基于时间结构的方法;神经启发方法(包括神经形态计算)。
