Year: 2024

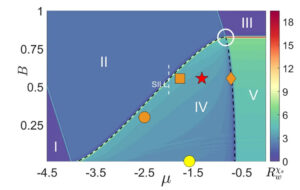
本篇研究来自西北大学张堃和郝昆课题组。基于量子门的四面体几何表示，本研究工作系统地展示了辫子门和Yang-Baxter门的非局域性质。研究发现辫子门和Yang-Baxter门仅出现在量子门四面体表示的特定边与面，即只有部分量子门与辫子门和Yang-Baxter门局域等价。另一方面，辫子门和Yang-Baxter门的几何表示可以给出其量子门分解的最优形式，为量子计算机上实现辫子门和Yang-Baxter门提供了理论基础。 文章介绍 Geometric representations of braid and Yang-Baxter gates Kun Zhang（张堃）, Kun Hao（郝昆）, Kwangmin Yu, Vladimir Korepin and Wen-Li Yang（杨文力） 通讯作者： 郝昆，西北大学现代物理研究所   研究背景： 量子反散射方法（Quantum Inverse Scattering Method）是求解量子可积模型的重要方法，其中Yang-Baxter方程是这一理论框架的核心。另一方面，随着量子信息理论的蓬勃发展，越来越多的研究揭示了量子可积模型与量子线路模型之间的深刻关系。Yang-Baxter方程的幺正解可以视作量子线路中的门操作，称为Yang-Baxter门。由Yang-Baxter门构成的有序量子线路被证明是Yang-Baxter可积的，而使量子计算机成为研究量子可积系统动力学新的有力工具。但是Yang-Baxter门作为一类特殊的量子门，其性质和构造却缺乏系统性的描述。本研究拟通过计算Yang-Baxter门的非局域参数，从而得到了Yang-Baxter门的几何四面体表示。分析其几何表示，可以进一步揭示Yang-Baxter门与其它量子门之间的关系。这项研究将为量子可积线路的深入探索提供理论支持，并有望为理解量子线路的可积性和设计新型量子算法奠定基础。   研究内容： 两量子比特门作为SU(4)群的群元素，可由三个实参数确定其非局域性质，称为两量子比特门的非局域参数。三个实参数构成了两量子比特门的三维几何表示，即量子门四面体。非局域参数相同的两量子比特门，可由单量子比特门变换得到，也称为局域等价。另一方面，非局域参数可以确定两量子比特门的最优分解形式，例如从CNOT门的非局域参数出发，可证明任意两量子比特门可以由最多3个CNOT门加上单量子比特门构造。 我们从四类幺正的辫子群表示出发，即两量子比特辫子门，计算了其非局域参数，发现了其中三类辫子门只出现在量子门四面体的一边，即局域等价。通过Yang-Baxterization方法，从此四类辫子门出发，我们构造了十类Yang-Baxter门。通过计算其非局域参数，我们发现十类Yang-Baxter门只出现在以下区域。   从Yang-Baxter门的几何表示出发，我们发现了当Yang-Baxter门中的谱参数与q变形参数取特殊值时，Yang-Baxter门也可以是其它特殊两量子比特门，包括Clifford门，Matchgate，和Dual-unitary门。Yang-Baxter门与以上特殊两量子比特门的交集暗示了由其构成的量子线路具有特殊的动力学特征。借助辫子门和Yang-Baxter门的非局域参数，我们构造了其关于CNOT门的最优分解，为辫子门和Yang-Baxter门在量子计算机上的实现提供了理论指导。 作者介绍 张堃  副教授 西北大学 张堃，西北大学物理学院副教授，2022年博士毕业于纽约州立大学石溪分校。主要研究方向为量子信息理论，包括量子算法，量子热力学，以及量子信息动力学等。   郝昆  研究员 西北大学 郝昆，西北大学现代物理研究所研究员，2013年博士毕业于本校现代物理研究所， 2018-2021年在纽约州立大学石溪分校从事博士后研究。主要研究方向为量子可积模型，近年来聚焦于量子信息、高能物理等前沿领域中新的物理模型的可积性研究。 期刊介绍 Journal of Physics A: Mathematical and Theoretical 2023年影响因子：2.0  Citescore：4.1 Journal of Physics A:...

Physics in Medicine & Biology（PMB）期刊由IOP出版社和医学物理与工程研究所（IPEM）合作出版。近日，我们采访了PMB期刊执行编委之一，来自美国约翰斯霍普金斯大学医学院放射肿瘤治疗与分子放射科学系的贾珣教授，让我们一起来看看他对期刊以及领域发展的见解吧。 访谈详情 1. 您为什么选择从事相关的领域研究？ 放射肿瘤学中的医学物理学是一门跨学科的研究领域。它综合了物理学、工程、计算技术和医学，为癌症患者提供创新、精准的治疗方法。这种多学科融合不仅提升了治疗效果，也推动了医学物理学在临床中的实际应用。作为一名获得美国放射学会（ABR）认证的临床物理师，我深入参与到临床实践，有机会发现和理解其中的需求和问题。这种亲身经历使我能够更好地利用物理和工程学手段来设计解决方案，以应对临床挑战。更重要的是，看到自己的研究成果应用到临床中，能够直接提高患者的治疗效果和生活质量，这种成就感十分宝贵。   2. 您目前从事的研究工作有哪些？ 我当前主要研究方向为医学图像重建与处理，多尺度放射疏运的计算机模拟与生物学建模，人工智能在医学图像与放疗中的应用，以及前临床多模态影像引导的小动物放疗平台开发。   3. 您认为五年后该领域的研究重点将会是什么？ 未来五年，我个人认为放射肿瘤学中医学物理的研究重点将有两个关键方向： （1）人工智能驱动的定量化，自动化与个性化：AI技术的进步将使得诊断，治疗，与评估更定量话，推动治疗流程的自动化，提高治疗效果、效率和安全性。此外，AI还将促进治疗的自适应和个性化发展，定制出更加个体化的治疗方案，从而提高疗效，减少副作用，进一步推动“量身定制”的精准医疗。 （2）生物学与放疗技术的结合：传统的放疗方法主要依赖物理手段破坏肿瘤细胞，而未来的研究将探索将放疗与生物学方法相结合。例如，放疗与免疫疗法结合，靶向放射性药物的应用等。   4. 是什么吸引您加入PMB期刊编委团队? （1）学术声誉与专业标准：PMB在医学物理学领域享有很高的学术声誉，以严格、专业的审稿流程闻名。编委团队积极、严谨地对待行业的热点，确保刊登的研究具备创新性和学术价值，这种严谨的学术氛围非常吸引我。 （2）推动领域科研发展：参与期刊的建设是一个能够直接贡献于学科发展的机会。通过支持优质论文的发表和学术标准的提升，我希望推动医学物理学新知识和新技术的传播，为行业科研的进步做出实质贡献。 （3）提升自身科研水平：通过参与PMB的编委工作，了解最新的学术动态和技术进展。与其他专家和研究者的交流合作不仅拓宽了我的学术视野，也促使我在自身研究中追求更高的创新性和严谨性。   5. 您认为像PMB期刊这样的期刊对领域的发展有什么重要影响？ （1）促进最新研究成果的交流：作为核心期刊，PMB为科研人员提供了展示和分享最新研究成果的平台，推动学科内和跨学科的交流。 （2）保障学术严谨性：PMB始终坚持严格的同行评审标准，积极谨慎的对待行业热点，效维护了学科的科学严谨性和学术公正性。 编委介绍 贾珣  教授 美国约翰斯霍普金斯大学 贾珣，现任美国约翰斯霍普金斯大学医学院放射肿瘤治疗与分子放射科学系教授、首席医学物理师。1999-2003年北京大学物理学院学士。2003-2009年美国加州大学洛杉矶分校物理学博士。主要研究方向为医学图像重建与处理，多尺度放射疏运的计算机模拟与生物学建模，人工智能在医学图像与放疗中的应用，以及前临床多模态影像引导的小动物放疗平台开发。发表学术文章190余篇。主持美国NIH多项研究课题。2017年获得美国医学物理学会（AAPM）John Laughlin青年科学家奖。2023年当选AAPM会士。自2017年起担任Physics in Medicine and Biology杂志执行编委。 期刊介绍 Physics in Medicine and Biology 2023年影响因子：3.3  Citescore：6.5 Physics in Medicine & Biology（PMB，《医学和生物学中的物理学》）由IOP出版社和医学物理与工程研究所（IPEM）合作出版，内容包括：放射物理学；辐射剂量学（电离和非电离辐射）；生物医学成像（如X射线、MRI、超声、光学，核医学）；图像重建和动力学建模；图像分析和计算机辅助检测；辐射医学应用；疗法（包括非电离辐射）；生物医学光学；辐射防护；放射生物学等。

本篇研究来自华中科技大学张新亮和李培宁课题组，探讨了扭曲混合维度MoO3结构（薄层/厚层MoO3同质结）中的横向光学力。通过调整入射光的偏振角、入射角以及MoO3的扭转角度，研究人员可以精确控制横向光学力的方向和强度，尤其在中红外频段表现出卓越的控制能力。这项研究为在纳米尺度上操控微小物体提供了一种全新的方法，具有广泛的应用前景。 文章介绍 Configurable lateral optical forces from twisted mixed-dimensional MoO3 homostructures Qizhi Yan（严其志）, Runkun Chen（陈闰堃）, Peining Li（李培宁） and Xinliang Zhang（张新亮） 通讯作者： 李培宁，华中科技大学 张新亮，华中科技大学/西安电子科技大学   研究背景： 通过电磁场与物质的动量交换，产生的光学力使得操控微小物体成为可能，并已应用于病毒捕获、单细胞操作和光力显微镜等领域。近年来，横向光学力，即垂直于光传播方向的力，受到了极大关注，它能使微小颗粒在光的入射平面上横向移动。横向光学力的产生通常与横向方向上的对称性破坏有关，这可能由散射体的几何形状或入射光场引起。为此，需要开发具有非对称电磁模式和大横向动量的结构和材料。而极化激元，尤其是双曲声子极化激元，具有强电磁场增强和高动量，能够施加较大的力。其中MoO3作为双轴二维材料，在中红外波段支持双曲声子极化激元传输，此外通过二维材料的堆叠可以打破电磁场的对称性。这些特性使其成为产生横向光学力的理想平台。   研究内容： 本研究从理论上提出并分析了在扭转的混合维度MoO3结构中产生的横向光学力。这种混合结构通过上下MoO3层之间的相互作用，生成了一种低对称性的声子极化激元。这种独特的电场和动量分布，可以产生较大且可控的横向光学力，从而更简单、高效地操控纳米颗粒。 研究通过数值模拟和理论计算，详细展示了这种横向光学力的调控能力。结果表明，通过调整MoO3层之间的扭转角度，以及改变入射光的偏振，可以精确控制横向光学力的大小和方向。在特定的入射和扭转角度条件下，声子极化激元可以实现单向传输，产生的横向光学力可达到近2×10-20 N/W·cm²，比自由空间中的光学力强约12000倍。此外，随着扭转角度的变化，声子极化激元的动量分布也随之变化，使得光学力的方向和强度可以进一步优化。 这一发现为纳米尺度上的光学操控提供了一种新的方法，特别是在操控微小颗粒和纳米制造方面展示了巨大潜力。研究还表明，通过光诱导力显微镜（PiFM）有望观察到三维光学力的效果。这种横向光学力调控技术不需要复杂的纳米制造工艺，操作简便，而且在中红外波段有效。它为非接触式操控纳米颗粒和活细胞等微小物体提供了新的技术工具。 作者介绍 李培宁  教授 华中科技大学 李培宁，华中科技大学教授、博士生导师。德国亚琛工业大学博士、西班牙CIC Nanogune纳米中心玛丽居里学者研究员。长期从事近场光学、微纳光子学研究，在Nature (3篇)、Science (2篇)、Nature Nanotechnology (2篇)、Nature Materials、Nature Photonics、eLight、 Nature Review Physics、Nature Communications (8篇) 、Science Advances等高水平学术期刊发表基础研究成果多篇。研究成果入选2018、2021年中国光学十大进展（基础研究类），入选美国光学学会“Optics in 2021”年度光学进展并被选为封面工作亮点推荐。得到多项荣誉和奖励的肯定，包括“国家优秀自费留学生奖学金”、“欧盟玛丽居里学者奖”和国家海外高层次人才计划青年项目。承担和参与国家自然基金，重点研发计划，湖北省杰青等基金，担任《香山科学会议》近场光学学科研讨会共同执行主席。   张新亮  教授 西安电子科技大学/华中科技大学 张新亮，西安电子科技大学/华中科技大学教授，国家杰出青年基金获得者，长江学者特聘教授，国家创新领军人才，美国光学学会Fellow。长期从事光电子器件与集成方面的研究工作，先后主持国家杰出青年基金项目、基金委重大国际合作项目、基金委重点基金项目、基金委重大科学仪器研制项目、国家重点研发计划项目等，发表了国际主流期刊论文350余篇，Web of Science统计引用6000余次，Google Scholar统计引用8000余次，先后主持和参与获得省部级自然科学一等奖4项。曾任华中科技大学副校长，现任西安电子科技大学校长。 期刊介绍 Journal of Optics...

特刊详情 客座编辑 Andreas Rosenkranz, 智利大学 Sana Munir, 智利大学   主题范围 This focus issue aims to shed light on 2D nanomaterials to highlight the latest advancements in rapidly evolving fields. The collection features articles on the synthesis, characterization, and application-related research using various 2D nanomaterials, including graphene, graphene oxide, MXenes, and transition metal dichalcogenides. These nanomaterials...

我们很高兴地宣布，IOP出版社新推出的开放获取机器学习期刊系列现已正式开放投稿：   Machine Learning: Engineering Machine Learning: Earth Machine Learning: Health   如果您的研究重点是机器学习、人工智能和数据驱动的计算方法在工程、地球、环境科学、医疗保健和生物工程领域的应用，欢迎您向以上期刊投稿！您的文章将有机会发表在我们的创刊号上！ 此外，IOP出版社目前为这些新期刊免除所有文章出版费用，您可以免费以开放获取的方式发表您的研究文章。 主编介绍 Jay Lee 美国马里兰大学 “Machine Learning: Engineering期刊致力于利用人工智能推动新技术与创新，构建多样化计算设备的知识体系，影响广泛的应用领域。通过预测并避免各种工程系统中隐匿的问题，最终打造一个无忧且具有韧性的工业系统和工作环境。”   Pierre Gentine 美国哥伦比亚大学 “Machine Learning: Earth期刊聚焦于创新方法，以提升我们对大气、海洋、生物圈、水圈、冰冻圈和地圈等复杂相互作用的建模、预测和管理能力。期刊欢迎AI在地球系统中的应用，同时也关注算法方面的创新。”   Jimeng Sun 美国伊利诺伊大学厄巴纳-香槟分校 “Machine Learning: Health期刊旨在成为推进和推广AI与机器学习方法、系统及应用的首选资源，真正改善全球健康与福祉。我们的目标是为研究人员和实践者提供一个平台，展示创新成果，并激发全球健康领域与AI及机器学习领域的协作。” 为什么选择在机器学习期刊系列上发表文章？ 广泛的多学科覆盖范围：该期刊系列覆盖广泛领域，汇聚所有从事机器学习和人工智能研究的社群。 提升研究影响力：通过完全开放获取的形式发表您的论文，最大程度地扩大研究的传播范围。目前，IOP出版社承担所有开放获取出版费用，因此该期刊对作者和读者均免费。 高质量的文章标准：严格的编辑标准，致力于发表在专业领域内具有重大突破的研究成果。 严格的同行评审：IOP出版社邀请来自全球的专家审稿人们进行严格的同行评审，保证高质量的在线出版工作，并由期刊专业的编辑委员会支持。 学会所有：IOP出版社是一家世界领先的学会出版社，获取的所有利润都将回馈给英国物理学会（IOP），用于支持世界各地的研究、教育和推广活动。 期刊介绍 Machine Learning: Engineering Machine Learning: Engineering是一本多学科开放获取期刊，致力于在所有工程领域应用机器学习、人工智能数据驱动的计算方法。该期刊还发表介绍机器学习和人工智能在方法、理论或概念上的进展，并将其应用于所有工程领域的研究。 Machine Learning: Earth Machine Learning: Earth是一本多学科开放获取期刊，致力于在地球、环境、气候科学、可持续发展的所有领域应用机器学习、人工智能和数据驱动的计算方法。该期刊发表应用数据驱动方法的研究报告，这些方法提高了我们对地球系统的认识，以及对生物圈、水圈、冰冻圈、大气圈和地圈之间相互作用的认识。 Machine...

本篇研究来自同济大学物理科学与工程学院齐润泽课题组。本文主要介绍了用于30.4nm高次谐波选择的窄带Mg/SiC多层膜，详细阐述了这一元件的设计、制备与表征工作。通过利用布拉格定律中的高级次设计，同时优化Mg/SiC多层膜中SiC的占比，获得了带宽仅有0.71nm的窄带Mg/SiC多层膜。通过模拟，这种窄带元件可以在实际应用中获得更好的高次谐波选择性，为其他波段的类似元件也提供了设计与制备思路。 文章介绍 Narrowband Mg/SiC multilayer mirror working as high-harmonic selector at 30.4 nm wavelengthZhe Zhang（张哲）, Runze Qi（齐润泽）, Qiushi Huang（黄秋实）, Yufei Feng（冯宇飞）, Zhong Zhang（张众）, Tonglin Huo（霍同林）, Hongjun Zhou（周洪军） and Zhanshan Wang（王占山） 通讯作者： 齐润泽，同济大学物理科学与工程学院，先进微结构材料教育部重点实验室，精密光学工程技术研究所   研究背景： 高次谐波光源（High-Harmonic Generation，HHG）能够将激光波长从可见光扩展到极紫外甚至软X射线的范围，这使得高相干性的短波光源不再局限于传统的大型科学装置，如：同步辐射光源和自由电子激光等。此外，HHG光源的相干性也比同步辐射光源更好，这可以更好的实现一些科学应用，如：时间分辨和角度分辨光电子谱、相干衍射成像等。HHG光源通常会产生一系列谐波，像一把梳子，谐波之间的间隔基于泵浦光源的波长。在大多数应用中，需要选出一个谐波满足应用的单色性要求，同时还要抑制相邻谐波。目前，获取单次谐波束的方法主要有两类：一种是光栅，另一种就是多层膜。多层膜由于其效率远高于光栅而受到研究者们的关注。因此，本文针对30.4nm附件的谐波选择开展窄带多层膜研究。   研究内容： 本文针对30.4nm的高次谐波开展窄带多层膜研究，希望通过窄带宽实现更好的谐波选择。首先，利用选择不同布拉格级次以及优化SiC材料占比的方式，设计出具备窄带宽的Mg/SiC多层膜，从理论上验证了缩小带宽的可行性。其次，利用直流磁控溅射的方法，根据设计参数制备了满足不同布拉格级次的Mg/SiC多层膜。然后，利用X射线衍射仪，干涉仪以及合肥同步辐射光源的极紫外反射率计对多层膜进行了结构、力学以及光谱性能的表征。结果表明，窄带最窄的Mg/SiC多层膜（三级次）带宽仅为0.71 nm的，其光谱分辨可达λ∕Δλ=42，远高于一级次Mg/SiC多层膜（带宽约为1.26 nm，λ∕Δλ=24）。此外，发现高布拉格级次的Mg/SiC多层膜无论是从成膜情况、界面粗糙度还是力学性质等方面皆可于常规Mg/SiC多层膜（一级次）相似，这验证了窄带多层膜在实际应用场景中具备良好的可行性。 基于以上的结果，对窄带Mg/SiC多层膜在大入射角下工作情况下的光谱相应进行模拟。结果表明，在大入射角度的工作场景下，高布拉格级次的Mg/SiC多层膜在30.4 nm左右具有更好的谐波选择性。 作者介绍 齐润泽  助理教授 同济大学 齐润泽，博士，同济大学物理科学与工程学院助理教授，主要从事极紫外与X射线、中子光学薄膜元件技术及相关研究，研究成果已应用于：德国BESSY II光源，上海同步辐射光源，东莞散裂中子源，中国工程物理研究所等多家科研机构。依托极紫外薄膜元件技术，以副总工程师身份参与研制中国科学院SY01星-STURI空间载荷的研制项目。 期刊介绍 Journal of Optics 2023年影响因子：2.0  Citescore: 4.5 Journal of Optics（JOPT）出版光学方面的实验和理论研究论文，研究领域包括：纳米光子学和等离激元光子学；超构材料和结构化光子材料；量子光子学；生物光子学；光与物质的相互作用；非线性和超快光学；光的传播、衍射和散射；信息和通信光学；集成光学；光伏和能量收集。除原创性研究外，JOPT还出版专题综述，为研究人员带来高质量的内容。所有JOPT文章还提供HTML阅读模式，方便研究人员使用手机或平板进行阅读。

特刊详情 客座编辑 Patrick Ravines，美国纽约州立大学布法罗分校 Chris Brown，美国伍斯特理工学院   主题范围 This STMP special issue is dedicated to the unique surfaces that make up works of art and cultural heritage. Surfaces cover everything, and come in all sizes and shapes with a wide range of properties and functions such as appearance, friction, adhesion, heat transfer, reactivity, and many...

本篇研究来自北京信息科技大学赵明镜课题组。本文主要研究二维和三维系统中斜信息量子相干的量子不确定性关系，通过量子态的纯度和标准正交基之间的交叠解析的给出量子相干的下界。我们希望这个工作能推动高维系统中量子不确定性关系的研究，并能够应用到量子干涉以及参数估计中。 文章介绍 The quantum uncertainty relation for skew information of coherenceMing-Jing Zhao（赵明镜）, Jie Cui（崔杰） and Yuan Sun（孙源） 通讯作者： 赵明镜，北京信息科技大学   研究背景： 量子相干是由量子态叠加产生的一种物理特性，也是量子理论中的一个基本概念，它在量子信息进程以及量子生物中发挥着重要作用，因此对量子相干的刻画和量化具有重要的研究意义。量子相干的大小依赖于测量基的选择，量子不确定性关系主要研究不同测量基下量子相干之间的约束关系。我们将探索量子态的纯度和标准正交基之间的交叠对量子不确定性关系的影响。本文主要研究二维和三维系统中斜信息量子相干的量子不确定性关系，通过量子态的纯度和标准正交基之间的交叠解析的给出量子相干的下界。我们希望这个工作能推动高维系统中量子不确定性关系的研究，并能够应用到量子干涉以及参数估计中。   研究内容： 本文主要研究二维和三维系统中斜信息量子相干的量子不确定性关系，研究方法是将寻找量子不确定性关系的下界问题转化为凸函数在凸集上的最大值问题。首先，在二维系统中，我们通过量子态的纯度和两组标准正交基之间不可兼容性建立了斜信息量子相干的量子不确定性关系。该下界对于非最大混合态或不可兼容的标准正交基是严格大于0的。该下界严格优于[Quantum Inf. Process. 22, 6 (2023)]中给出的量子不确定性关系。然后，在三维系统中，我们通过量子态的纯度和两组标准正交基之间的3个交叠建立了斜信息量子相干的量子不确定性关系。本文建立的量子不确定性关系揭示了量子态的纯度和标准正交基之间的交叠对量子相干的影响。本文提出的研究方法对于其他度量的量子不确定性关系的研究有一定的借鉴作用。 图：在三维系统中，对于纯态|φ⟩=α|0⟩+β|1⟩+γ|2⟩，α,β,γ∈R，选取两组标准正交基X={|0⟩,|1,|2⟩}和Y={|y1⟩,|y2⟩,|y3⟩}，其中|y1⟩=-√2/4|0⟩+√2/4|1⟩+√3/2|2⟩，|y2⟩=-√2/2|0⟩+√2/2|1⟩，|y3⟩=√6/4|0⟩-√6/4|1⟩+1/2|2⟩。图中上面的平面是本文得到的量子不确定性关系的下界，下面的曲面是[Commun. Theor. Phys. 71, 1443 (2019)]得到的量子不确定性关系的下界。由图像可以看出本文得到的下界的优势。 作者介绍 赵明镜  教授 北京信息科技大学 赵明镜，北京信息科技大学教授，硕士生导师，长期从事量子信息的理论研究。2011年毕业于首都师范大学获得理学博士学位，曾在德国马克普朗克应用数学研究所从事博士后研究，加拿大圭尔夫大学进行学术访问。 期刊介绍 Journal of Physics A: Mathematical and Theoretical 2023年影响因子：2.0  Citescore：4.1 Journal of Physics A: Mathematical and...

特刊详情 客座编辑 Diego Abalos，丹麦奥胡斯大学 Klaus Butterbach-Bahl，丹麦奥胡斯大学 Jørgen Eivind Olesen，丹麦奥胡斯大学 主题范围 Thanks to the application of nitrogen (N) fertilizers, farmers tripled global crop production while the cultivated land area only increased by 30%. However, by 2050 the global food demand will further increase, and therefore the demand for N inputs and for agricultural land are expected...

本篇研究来自中国科学院大气物理研究所刘屹岷研究员课题组。本研究基于线性回归方法，定量评估了热带印度–太平洋和北大西洋海温异常、局地土壤湿度反馈以及全球增暖对2022年夏季中国东部极端高温的相对贡献。结果表明局地持续偏干的土壤湿度对7–8月极端高温的发生起着最重要的作用。本研究将有助于深化对中国东部夏季极端高温形成机制的理解。 文章介绍 Extreme heatwave over Eastern China in summer 2022: the role of three oceans and local soil moisture feedback Jilan Jiang（姜继兰）, Yimin Liu（刘屹岷）, Jiangyu Mao（毛江玉） and Guoxiong Wu（吴国雄） 通讯作者： 刘屹岷，中国科学院大气物理研究所   研究背景： 2022年夏季，中国东部遭遇了自1961年以来最强且持续时间最长的极端高温，给人民生活和社会经济的发展造成了严重影响，受到科学界的广泛关注。伴随着极端高温的发生，热带太平洋发生了拉尼娜事件，热带印度洋出现了负印度洋偶极子模态以及北大西洋有三极型海温发展。这些海温异常以及局地持续偏干的土壤湿度对此次极端高温发生发展的相对贡献尚不清楚。因此，定量评估三大洋和局地土壤湿度对中国东部夏季极端高温发生的相对贡献以及协同作用是非常有必要的。   研究内容： 本研究表明，2022年6月的极端高温主要集中在长江流域以北，其中线性趋势代表的全球增暖对温度异常的贡献约为40%，而三大洋海温异常与局地土壤湿度的协同贡献约为10%。一次次同位相天气尺度罗斯贝波的传播可能是导致此次极端高温的主要原因。 在7–8月，极端高温主要发生在长江流域，其中局地土壤湿度反馈的贡献最大，分别约为42%和66%。其次，全球增暖分别贡献了36%和28%。北大西洋三极型海温异常通过激发中纬度定常罗斯贝波列，促进中国东部上空异常反气旋的发展，对温度异常的贡献均约为10%。在7月，热带印度–太平洋海温异常通过纬向沃克环流以及起源于海洋性大陆地区的经向环流促进了中国南方下沉运动和高温异常的发展，其贡献约为10%。而在8月，该海温异常促进了西北太平洋反气旋的发展，但对温度异常的直接贡献非常小，仅为1%（图1）。   图1 2022年（a）7月和（b）8月极端高温形成机制示意图。其中百分数表示各强迫的定量贡献 本研究的创新之处在于基于线性回归方法，定量评估了三大洋和局地土壤湿度对2022年夏季中国东部极端高温的相对贡献。研究发现，持续性极端高温的发生依赖于多因子的协同作用，其中局地持续偏干土壤湿度的正反馈作用尤其不可忽视。此外，中国极端高温形成机制的季节内变化也值得关注。本研究将有助于深化对中国东部夏季极端高温形成机制的理解。 作者介绍 刘屹岷  研究员 中国科学院大气物理研究所  刘屹岷，中国科学院大气物理研究所，研究员，国家杰出青年科学基金和全国百优论文获得者，主要从事副热带天气气候动力学、青藏高原天气气候动力学、极端天气气候事件、海气相互作用以及数值模拟研究。   姜继兰  博士后 中国科学院大气物理研究所 姜继兰，中国科学院大气物理研究所，博士后，目前主要从事极端天气气候事件、海气相互作用以及复杂气候网络方面的研究。 期刊介绍 Environmental Research Letters 2023年影响因子：5.8  Citescore:...

IOP出版社旗下期刊Environmental Research: Water近日宣布中国科学院地理科学与资源研究所冷国勇研究员加入该刊编委会，担任编委。我们在此表示热烈欢迎！ 编委介绍 冷国勇  研究员 中国科学院地理科学与资源研究所 冷国勇，中国科学院地理科学与资源研究所研究员，博士生导师，中国科学院特聘核心骨干，国家高层次人才引进计划青年项目入选者。主要从事水文气象、农业水文、气候变化等方面的研究。获教育部自然科学奖一等奖。 期刊介绍 Environmental Research: Water Environmental Research: Water是一本多学科、开放获取的期刊，致力于解决与水相关的重要挑战，并在全球变化、环境关联系统、复原力、环境减缓、环境适应、环境安全和最广泛意义上的解决方案方面进行努力。

近日，精密测量院研究员管习文和博士研究生罗佳佳，以及美国莱斯大学教授浦晗合作，在一维排斥哈伯德模型理论研究方面取得重要进展。研究人员给出了该模型的分数化自旋和电荷激发、自旋相干和非相干Luttinger液体、相互作用驱动的量子相变和量子制冷等重要的精确结果。该研究成果9月16日在国际物理学领域知名期刊Reports on Progress in Physics上发表。 文章介绍 Exact results of the one-dimensional repulsive Hubbard model Jia-Jia Luo（罗佳佳）, Han Pu（浦晗） and Xi-Wen Guan（管习文）   通讯作者： 管习文，中国科学院精密测量科学与技术创新研究院   研究背景： 长期以来，描述晶格上相互作用电子的费米哈伯德模型一直是量子多体物理学中的重点研究领域，这主要是因为该模型可以用来描述普适的基本物理现象以及刻画某些量子材料的特性。最近，光晶格中的超冷原子对测量超导性和超流性等奇异现象提供了有效方法。特别是，用超冷原子成功地实现了一维(1D)精确可解哈伯德模型，例如，在费米哈伯德模型中观察到了一维自旋与电荷的动力学传播及超扩散现象。然而，理解费米子之间的相互作用是如何影响自旋和电荷的相干和非相干量子态，以及如何严格地构建相互作用驱动的量子相变、莫特绝缘体和普适热力学关系仍然是世界公开挑战性难题。在这种情况下，精确可解的一维费米哈伯德模型通常被人们期待用来为重要普适规律提供基准性参考，例如，分数化自旋和电荷激发、自旋相干和非相干Luttinger液体、相互作用驱动的量子相变和输运特性等。尽管该模型的精确解Bethe ansatz方程已有76年的研究历史，但求解1D Hubbard模型的Bethe ansatz方程仍然是众所周知的困难，阻碍了人们对其涌现的多体量子现象的认知和在量子科技的应用。   研究内容：   磁化率威尔逊系数精确刻画了一维哈伯德模型的相图。低温下不同相区对应不同常数的威尔逊系数，其仅仅由Luttinger参量、电荷和自旋的声速决定，揭示了量子液体的本质。I：真空态；II：部分填充的全极化相区；III：半填充的全极化相区；IV：部分填充的部分极化相区；V：半填充的莫特绝缘体。论文中给出了相图中符号标记处的自旋和电荷分数化激发谱。     (a) 化学势-相互作用驱动下粒子数密度的三维图，给出了相区I, 相区IV(或II)与相区V(或III)之间的相变。绿色箭头表示相区IV至相区V的相互作用驱动的量子相变；（b）为相互作用驱动的相区IV至相区V中粒子数密度的标度行为，解析与数值计算完全吻合   在该工作中，博士研究生罗佳佳在管习文和浦晗的指导下，经过4年多的科学研究，取得的主要成果如下： 1、精确获得了自旋非相干液体的重要特征，解析计算了单粒子格林函数，表明电荷自由度关联随距离呈幂律衰减，而自旋自由度关联在距离上呈指数衰减。 2、严格推导出了Luttinger液体区的热力学和磁学的普适规律、自旋非相干液体的热力学以及标度函数。 3、首次提出关于格点模型的Tan Contact（谭接触），作为其特殊的热力学量，建立了Tan Contact磁化率与密度、磁化强度和熵的变化之间的重要联系，从而提供了精确描述相互作用驱动的量子相变、Mott绝缘体、热效应和量子制冷。 这些结果为高维Hubbard模型提供了基准性参考。他们的研究方法和结果是全面的和新颖的，展现了理解量子多体物理现象的新视野。在文章接受发表后，马上引起Reports on Progress in Physics所涵盖研究领域读者的兴趣和引用，包括凝聚态物理学、数学物理学、原子和分子物理学、统计物理学、量子度量学等。针对相关研究结果，管习文于2024年受邀在物理学最具影响力的美国 “March Meeting”（美国物理三月年会）作特邀报告。 相关研究成果以“Exact results of one-dimensional...