JPhysD编辑优选:均匀波导中自旋波的传播特性及其应用研究
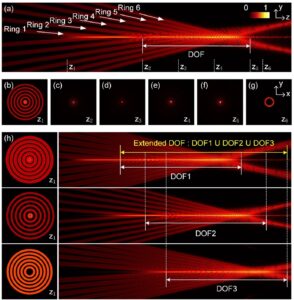
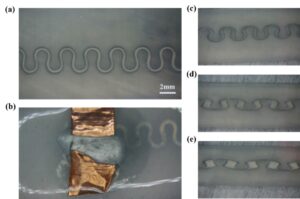
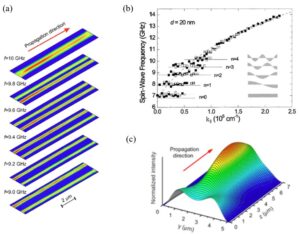
本篇研究来自电子科技大学钟智勇课题组。本文综述了相干自旋波在均匀波导中传播现象效应以及均匀自旋波波导的最新研究进展。 文章介绍 Spin wave propagation in uniform waveguide: effects, modulation and its application Lei Zheng(郑磊),Lichuan Jin(金立川),Tianlong Wen(文天龙),Yulong Liao(廖宇龙),Xiaoli Tang(唐晓莉),Huaiwu Zhang(张怀武),Zhiyong Zhong(钟智勇) 通讯作者: 钟智勇,电子科技大学电子薄膜与集成器件国家重点实验室 研究背景: 自20世纪60年代摩尔定律提出以来,微处理芯片上的晶体管数量几乎每两年增加一倍。然而随着互补金属氧化物半导体(CMOS)工艺逐步逼近物理极限,尤其是高密度晶体管所带来的热耗散问题,使得半导体集成电路的发展受到了严重的制约。因此国际半导体技术蓝图(ITRS)将关注点聚焦于物理层面的创新,指出基于自旋波的信息传输和数据处理是未来突破摩尔定律极限的重要技术路线之一。 自旋波,其量子态为磁振子(Magnons),利用磁矩的非一致进动,在导电或绝缘的磁性材料中可实现没有载流子定向移动的磁矩角动量传播,有效地克服了焦耳能耗的产生,为突破纳米级、高集成度、超低能耗的电子器件热耗散瓶颈问题开辟了一条崭新的途径,除此之外,自旋波在高频率(高达太赫兹)、短波长(短至几纳米),以及易于实现的多种非线性效应等方面具有其他技术不可替代的优势,被学界认为其在未来高速低能耗计算、绝缘体自旋电子学、微纳磁振子学、微波及太赫兹通讯和量子计算等领域中都有光明的应用前景。 自旋波器件由三部分组成:自旋波激励源、自旋波波导以及自旋波探测器。自旋波波导作为自旋波器件的关键部分,其所起到传播和调制自旋波的功能。典型的自旋波波导包括均匀波导和磁振子晶体。均匀波导通常是指由同一种连续磁介质构成的波导,磁振子晶体则是类似于光子晶体的人工晶体。本文综述了相干自旋波在均匀波导中传播现象效应以及均匀自旋波波导的最新研究进展。 研究内容: 自旋波波导是自旋波器件的核心。通常,自旋波的传播特性及传播现象是通过自旋波波导中的色散关系来体现的。本文从自旋波在均匀波导中的色散关系出发,描述了例如自旋波信道化、量子化、自聚焦等特殊的传播现象(如图1)。紧接着,基于这些基本理论,本文从结构、外场和偶极场三个方面介绍了均匀波导中自旋波调制方法(如图2),并深入讨论了各类调制方法的应用及其局限性。例如微结构调制方法是适用于固定功能器件的设计,并且这类方法的调制效果稳定且较为高效;自旋转移矩效应( STT)及自旋轨道矩效应(SOT)效应调制方式可以有效地阻碍或放大自旋波的传输,这类调制方式的优点在于其快速响应速度,尽管利用STT和SOT效应调制都存在焦耳热的问题,但可以通过减小波导的宽度或将其集成到散热器设备中来减少焦耳热的产生。不同的自旋波调制方法具有不同的特点和应用场景。多种调制方法的结合可能是未来自旋波调制研究的主要方向之一。对自旋波的传播特性及调制方法的研究,推动了自旋波器件的发展,并取得了初步成功。与CMOS器件相比,自旋波器件在能量耗散和逻辑结构方面具有明显的优势。然而,自旋波器件的集成以及实现与CMOS电路的兼容性仍然面临巨大挑战。 图1 (a)自旋波信道化现象传播示意图。(b)自旋波量子化色散关系图。(c)自旋波自聚焦现象传播示意图 图2 (a)基于几何结构(缺陷)的自旋波调制方式。(b)基于SOT效应调制方式。(c)基于磁拓扑结构(磁畴)的自旋波调制方式。(d)基于偶极场的自旋波调制方式。 作者介绍 钟智勇,男,1970年5月生,教授,博士生导师。IEEE学会高级会员,《Journal of Material Science & Technology》学术期刊编委,四川省学术与技术带头人(2021年),教育部新世纪优秀人才(2008年)。主要研究方向包括纳米磁性材料与结构、自旋电子器件、功率与控制磁性器件和微波磁电子器件。 期刊介绍 Journal of Physics D: Applied Physics 2022年影响因子:3.4 Citescore:5.9 Journal of...